Ранг матрицы.

Рассмотрим матрицу 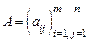размера m×n.

А= .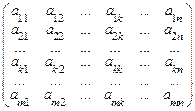

Выберем в ней к строк и к столбцов, к≤min { m,n }. Определитель, образованный элементами матрицы А, стоящими на пересечении выделенных строк и столбцов, называется минором к -го порядка матрицы А. обозначаем: М 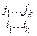, где i ₁, …, i_k - номера выбранных строк, а j ₁, …, j_k - номера выбранных столбцов. В матрице А выделен пунктиром минор к - го порядка

М = .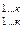

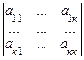Рангом матрицы А называется наивысший порядок миноров, отличных от нуля.

Обозначение: rang A=r (A)= r.

Базисным минором матрицы А называется отличный от нуля минор, порядок которого равен рангу матрицы. Базисный минор определяется не единственным образом.

Свойства ранга матрицы:

1. При транспонировании ранг матрицы не меняется.

2. Ранг матрицы не меняется при элементарных преобразованиях строк и столбов.

3. Нулевая строка (нулевой столбец) не влияет на ранг матрицы, при вычислении ранга матрицы ее (его) можно вычеркнуть.

Свойство 1 вытекает из того, что при транспонировании определители не меняются. Свойство 3 следует из того, что определитель, содержащий нулевую строку (столбец) равен нулю. Свойство 2 вытекает из соответствующих свойств определителей: при элементарных преобразованиях строк и столбцов определители, не равные нулю, а равные нулю- преобразуются в равные нулю.

Методы вычисления ранга матрицы.

1. Метод окаймляющих миноров.

Если найден минор к -го порядка М ≠0, то проверяем только те миноры (к+ 1)-го порядка, которые содержат (окаймляют) найденный минор. Если все они равны нулю, r (A)= k. Если же найдется отличный от нуля минор (к+ 1)-го порядка, процедуру повторяют.

2. Метод элементарных преобразований.

С помощью элементарных преобразований строк и столбцов приводим матрицу к эквивалентному виду:

~ ,

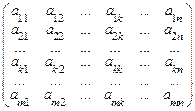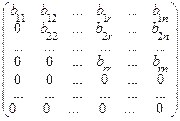где 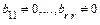(пунктиром выделен отличный от нуля минор M 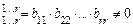), поэтому r(A)= r.

Пример 10.4. Найти ранг матрицы: а)методом окаймляющих миноров, б)методом элементарных преобразований, если дана матрица

.

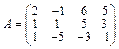Решение. а)Так как М 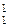=2 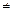0, то ранг матрицы не меньше единицы. Рассмотрим те миноры второго порядка, которые содержат минор М . В частности, 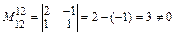и ранг матрицы не меньше двух.

Проверим те миноры третьего порядка, которые содержат 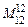. Их два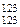: М и М (всего миноров третьего порядка – четыре).

,

.

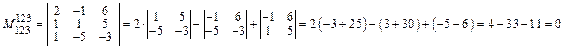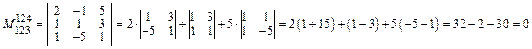Таким образом, все окаймляющие миноры третьего порядка равны нулю, а так как найден минор второго порядка 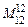, отличный от нуля, то r(A)=2.

Найденный минор 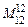– базисный; базисным также является минор .

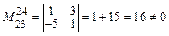В заключение приведем теорему, играющую важную роль в исследовании систем линейных алгебраических уравнений.

Теорема 10.1. (О базисном миноре).

Ранг матрицы равен рангу системы ее вектор- строк (вектор- столбцов). Система строк (столбов) матрицы, содержащая базисный минор, образует базис в системе вех строк (столбцов) матрицы.

Замечания. 1. Матрица А порядка n невырождена тогда и только тогда, когда r(A)= n.

2. Ранг системы векторов равен рангу матрицы, составленной из координат

векторов этой системы.

Дата добавления: 2015-07-20