некоторых физических зависимостей многочленами

Как без калькулятора быстро оценить с точностью до сотых сколько

1,015? Здесь нам смог бы помочь бином Ньютона. Действительно, формула в данном случае могла бы выглядеть так:

. А после подстановки x=0,01 и

n=5 надо было бы понять, что нас будут интересовать только два первых слагаемых, потому что вклад других в общую сумму явно не превышать одной сотой. Итак, 1,05. Если бы нужно было найти ответ с точностью до 0,0001, то достаточно было бы найти сумму трех слагаемых. В данном случае это делается без проблем устно. Сделайте соответствующие расчеты и сравните с результатом, полученным с помощью калькулятора. Удовлетворяет приближенрезультат условие на точность?

А что делать, если без калькулятора с точностью до одной десятитысячной

надо найти 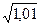? Вспомнив, что , попробуем вместо n

подставить 0,5. Первые три слагаемые дадут

.

Сверьтесь с калькулятором! Обратите внимание на то, что с числом 1,01 мы оперировали как с математически точным, а не как с приближенным числом физической величины. При обработке экспериментальных результатов находить или 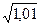с точностью до 0,0001 нет никакого смысла, если же число 1,01 найдено экспериментально с точностью до 0,005. А как быстро подсчитать сколько будет с точностью до сотых? Необходимо только понять, что в данном случае в выражении иметь x=-0,01, n=-2. Итак, получим 1,02. Проверьте!

Как видите, попытка воспользоваться формулой, которая была доказана для , в случаях, когда показатель степени выходит за пределы натуральных значений, дает обнадеживающие результаты. Выполнение заданий со «слайда» № 1.7а позволит подкрепить веру в то, что это не случайность.

При выполнении новых задач Вам придется пользоваться тем, что

, где - любое действительное число (). попробуем

доказать эту формулу хотя бы для натуральных значений показателя степени. Каким путем пойти?

Во-первых, можно попробовать воспользоваться методом математической

индукции, поскольку речь идет о натуральных степени, а формулу надо только доказать (гипотеза о ее виде в наличии). Обозначим показатель через n. Значит, надо доказать, что при . Проверка для n=1

выполняется без проблем. Действительно, , потому производная от суммы равна сумме производных, производная от константы (единицы) равна нулю, а от х - единице. Теперь нужно, предположив правильность формулы для n=k, доказать, что с этого следует правильность для n=k+1, т.е. . Продолжите доказательство, понимая, что , и вспомнив, как вычисляется производная от произведения двух функций.

Во-вторых, можно попытаться воспользоваться тем, что мы уже умеем

дифференцировать полином, и свести к необходимому виду выражение с помощью бинома Ньютона:

А что нам хотелось бы получить? . Что-то не очень

похоже! Но не будем отчаиваться и внимательнее присмотримся к первой

формуле. При k=0 выражение, стоящее под знаком суммы, равно нулю. Итак,

под знаком суммы можно вместо «k=0» написать «k=1». А теперь сделать

замену k=i+1. Тогда мы получим следующее: . Полного совпадения с тем, что надо, еще нет, но уже явно ближе. Осталось доказать, что . Продолжите доказательство, вспомнив формулу для биномиальных коэффициентов.

Мы воспользовались двумя уже знакомыми путями. Существует третий,

значительно короче и такой, который станет нам пригодится еще не раз. для него следует усвоить еще одну важную общую формулу дифференцирования. Речь идет о дифференцировки так называемой сложной функции.

Что может быть сложного в функции ? Просто ее можно подать

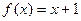как функцию, состоящую из двух: , где , а

.

На интуитивном уровне формулу дифференцирования сложной функции можно получить так: . Похоже на то, что числитель и знаменатель умножили на одно и то же. Не останавливаясь на строгом доказательстве подобного действия, обратим внимание на результат: производная от сложной функции представляется как произведение двух производных, причем первая - производная функции , для которой f является аргументом. В нашем случае , а .

Итак, . Понятно, что .

Например найдем производную функции . Представьте себе, сколько бы времени мы потратили, если бы попытались идти старым путем: подать функцию в виде полинома пятнадцатого степени, а затем дифференцировать полином по известной формуле. Но даже чтобы подать эту функцию в виде полинома с помощью бинома Ньютона, фактически пришлось бы пользоваться идеей, заложенной в понятии сложной функции.

Из каких же функций состоит заданная? Внешняя функция - степенная: . Далее - линейная: F=2f +8. Потом - снова степенная: . А дальше - снова линейная: . С линейными и степенными мы уже имели дело.

Значит, должно быть понятно, что

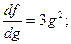
Итак, . Проверьте! Составьте свои упражнения и потренируйтесь с товарищами!

После таких тренировок можно приступать и к задачам «слайда» № 1.7а.

Обратите особое внимание на первое задание, которое ориентирует Вас на то, что общую формулу коэффициентов разложения функции в ряд Маклорена (за неотъемлемыми целыми степенями аргумента) можно вывести вполне самостоятельно. Эта формула пригодится для любой функции, которую можно бесконечное число раз

дифференцировать при x=0. А навыки разложения функции в ряд Маклорена

чрезвычайно важны при изучении и применении физики.

Отметим, что в пояснительной тексте «слайда» № 1.7а Вам встретится

отметка не только суммы (Σ), но и произведения (П). Как Σ, так и П - великие греческие

буквы («сигма» и «пи» соответственно). Помните, как выглядят маленькие?

Обратим также внимание на то, что использование общей формулы для

коэффициентов разложения функции в ряд Маклорена не всегда кратчайший

путь для их нахождения. Например, вычислить несколько первых коэффициентов разложения функции можно очень быстро, понимая, что они совпадать с коэффициентами так называемого биномиального ряда, для нахождения которых нет необходимости вычислять производные.

Примерам применения разложения функции в ряд Маклорена

для аппроксимации физических зависимостей посвященные задачи «слайда» № 1.7б. Почти все физические формулы, необходимые для выполнения задач, приведены в их условиях. Исключением является задание № 4, где надо знать общую формулу для потенциальной энергии тела массой m в гравитационном поле Земли на расстоянии h от ее поверхности. Попробуем ее вывести. По закону всемирного тяготения сила, с которой точечное тело притягивается к Земле, обратно пропорциональна квадрату расстояния между телом и центром Земли. В нашем случае это расстояние равно , где - радиус Земли. Кроме того, известно, что при h=0 сила тяжести равна mg, где g - ускорение свободного падения. Итак, сила будет уменьшаться при подъеме

тела от mg до .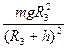

Потенциальная энергия по своему определению равна работе против силы

тяжести при подъеме тела от поверхности Земли до высоты h. А работа, в свою очередь, подсчитывается как интеграл: 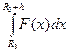, где . Выведите формулу для U(h)(или вспомните, что вы уже это фактически делали), а затемнайдите первые два слагаемых разложения этой функции в ряд Маклорена. Первоеслагаемое должно давать знакомое выражение mgh, а второе можно будет использовать дляоценки погрешности, которую делаем, не учитывая изменение силы тяжести с высотой.Другие слагаемые ряда будут слишком малыми при h=128 км и R=6400 км.

Для выполнения задач по «слайда» № 1.7б нет необходимости знать, откуда взялись приведенные физические формулы. На эти задачи можно смотреть как на чисто математические упражнения. Но для успешного дальнейшего обучения было бы полезнее, если вы поинтересовались их происхождением.

Дата добавления: 2015-07-11