Прямолинейного движения материальной точки

Применение идеи интегрирования для вычисления площадей и объемов

Геометрических объектов, а также работы силового поля в случае

прямолинейного движения материальной точки

Хоть мы ввели определенный интеграл как прирост определенной первообразной, нами было выяснено, что сама идея интеграции тесно связана с тем, что многие физических и геометрических величин являются аддитивными. Например, если мысленно разделить тело на несколько частей, то объем тела можно вычислить как сумму объемов его частей. То же можно сказать и о массе. А вот температура не является аддитивной величиной.

Мы уже упоминали формулу для площади круга (). А откуда она

взялась? Воспользуемся идеей интегрирования. Обратите внимание: не вычислим определенный интеграл, а воспользуемся идеей интегрирования! Разделим круг на большое количество маленьких секторов, каждый из которых напоминал бы равнобедренный треугольник с маленькой основой. Эта основа является хордой окружности, но она уже почти совпадает с дугой, которую взимает. Сделайте соответственные чертежи!

Конечно, если найдем сумму площадей треугольничков, то получим площадь

многоугольника, который вписан в круг, и площадь будет меньше площади соответственного круга. Но, уменьшая размеры треугольничков (и увеличивая их количество), будем получать многоугольники, площади которых все больше будут приближаться к площади круга. Понятно, что в предельном случае высоты всех треугольничков будут равны радиусу окружности, поэтому при нахождении суммы площадей эту величину можно как общий множитель вынести за знак суммы. Так

же можно вынести общий множитель 1/2, который входит в формулу для площади каждого треугольника (1/2ha – полупроизведение высоты на основание). Что же останется под знаком суммы? Только длины основ треугольничков, которые в сумме в предельном случае составят длину окружности! Если теперь вспомнить, что число вводится как

отношение длины окружности к ее диаметру, то можно записать ответ

площади круга радиусом R. Как получена формула для площади треугольника (1/2ha)? Сделайте чертеж, на котором было бы видно, что площадь треугольника вдвое меньше площади соответствующего прямоугольника. Но можно вывести эту формулу интегрированием.
Зачем? Потому что метод легко обобщить на случай вычисления объема

пирамиды! Разделим произвольный треугольник на тоненькие полоски, расположенные параллельно той стороны треугольника, которую мы будем считать основой (пусть ее длина равна a). Возьмем противоположную основы вершину треугольника по точку отсчета на оси Ох, которую направим в сторону основы перпендикулярно к ней. Сделайте соответствующее чертежи!

Как зависит длина тоненькой полоски от ее положения? То есть, какой вид имеет функция l(x)? Если обозначить высоту треугольника через h, то

l(h)= a. Понятно также, что l(0)=0, а функция l(x)- линейная (это следует из

сходства соответствующих треугольников). Значит, l(x)=(a*x)/h, а площадь полоски 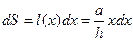. В такой записи мы учли, что ширина и площадь тоненькой полоски являются величинами дифференциально малыми. Осталось самостоятельно вычислить интеграл: .

Процедура вывода общей формулы для объема пирамиды аналогичная.

Если треугольник мы делили на тоненькие полоски, то пирамиду разделим на

тоненькие пластины. Ось Ох перпендикулярна к основанию. Линейные размеры этих пластин (не считая толщину) будут расти пропорционально их так же, как в случае с треугольником (это следствие сходства соответствующих фигур). А вот площади пластин будут расти пропорционально , потому площади подобных фигур пропорциональны

квадрату линейных размеров. Если площадь основания пирамиды обозначить через , то площадь пластины, что находится на расстоянии х от вершины пирамиды, будет , дифференциально малый объем будет равен

Соответственно, объем всей пирамиды выразится интегралом:

Вот и все расчеты! Как вычислить объем конуса, основой которого является круг радиусом R, а высота равна h? Достаточно в только найденную формулу подставить , потому что конус делить на тоненькие пластины можно так же, как и пирамиду! А как найти площадь сферы радиусом R? Достаточно просто для того, кто знает тригонометрические функции и легко находит от них производные и первоначальные! А можно провести вычисления без тригонометрических функций? Рассмотрим один «хитрый» способ. Разделим сферу на тоненькие кольца, рассекая ее параллельными плоскостями. Взяв центр сферы за точку отсчета, направим ось Ох перпендикулярно этим плоскостям. Вспомните, как выглядит географический глобус. Если представить, что ось Ох проходит через полюса, то линии пересечения плоскостей и сферы будут напоминать о параллелях, но расположены заметно плотнее, чем обычно на глобусе.

Найдем площадь dS одного тонкого кольца, центр которого находится на

расстоянии х от центра сферы, а расстояние между плоскостями, которые его «вырезают» равна dx. Если радиус кольца r, а ширина dl, то . Радиус как функцию х можно было бы найти с помощью теоремы Пифагора, но не будем спешить, а спросим себя: как через dx выразить dl (расстояние между двумя «параллелями», измеряемая вдоль «меридиана»)?

Сделайте чертеж сечения сферы плоскостью, содержащей ось Ох. Отметьте на нем величины R, r, dx, dl. Найдите подобные прямоугольные

треугольники, из сходства которых можно сделать вывод, что .

Конечно, дифференциально малый треугольник с гипотенузой dl и одним из катетов dx на чертеже будет иметь малые размеры по сравнению с треугольником, у которого гипотенуза R и соответствующий катет r. Начертите так, чтобы сходство треугольников, о которых говорится, можно было заметить. После подстановки dl в выражение для dS получим интересный результат: . Он означает, что площадь части сферы, которую «вырезают» две параллельные плоскости, зависит только от радиуса сферы и расстояния между этими двумя плоскостями. Если бы положение пластин задавался числами и 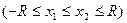, то соответствующая площадь равнялась бы . Если же

нам нужна площадь всей сферы, то нужно предположить, что 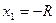, а . Тогда получим, что .

Найдем объем шара, радиус которой R? Рассмотрим два пути, которые

отличаются способом разделения шара на такие дифференциально малые элементы, объемы которых мы уже умеем вычислять. Зная формулу для площади сферы, можно понять, какого объема будет сферический слой радиусом r толщиной . Если теперь представить, что шар радиусом R разделен на большое количество концентрических сферических слоев, то станет очевидным, что объем шара подсчитывается так:

Второй способ похож на тот, которым мы вычисляли площадь круга,

разбивая на сектора, напоминающие равносторонние треугольники. Действительно, представим, что шар состоит из большого количества пирамидок, высоты которых равны почти R, а основы очень маленькие, но их суммарная площадь фактически равна площади сферы, ограничивающей шар. Вспомните о сумме основ треугольничков, которая в

предельном случае равна длине окружности, которое ограничивал круг! С

формулы площади сферы и объема пирамиды окончательно получим уже знакомую нам формулу для объема шара. В обоих рассмотренных нами подходах к вычислению объема шара мы опирались на известную формулу для площади сферы. Нельзя обойтись без нее? Достаточно выбрать другой путь для разделения шара на дифференциально малые элементы. Попробуем разделить шар на тонкие пластинки параллельными плоскостями, перпендикулярными к оси Ох. Радиус пластинки, положения которой

задается координатой х, определится из теоремы Пифагора: . Формула площади круга нам известна: . Соответственно, объем пластинки будет таким: . Остается проинтегрировать от -R до R, или от 0 до R, а затем результат умножить на 2 (шар состоит из двух полушарий!). Сделайте соответствующие вычисления!

А нельзя ли из формулы объема шара, выведенной последним способом,

получить формулу площади сферы? Вспомним, что, исходя из деления шара на тонкие концентрические сферические слои, можно записать:

Рассматривая правую и левую части этого равенства не как числа, а как функции, аргументом которых является R, можно найти от этих функций производные и приравнять их. Тогда получим:

Перейдем от примеров применения идеи интегрирования для вычисления

площадей и объемов геометрических объектов к физическим понятиям, введение которых нуждается в этой же идеи. Рассмотрим три связанных между собой понятия: механической работы, кинетической и потенциальной энергий материальной точки. Правда, есть и четвёртые понятие, тесно связанное с ними. Речь идет о так называемой полной

механической энергии, которая является суммой кинетической и потенциальной. Сейчас мы рассмотрим только случай прямолинейного движения. при этом будем считать, что сила, действующая на материальную точку, зависит исключительно от места нахождения точки на прямой в данный момент (которая фиксируется координатой l), а ее направление совпадает или противоположен направлению единичного вектора , который задает ориентацию прямой. Это означает, что можно

записать так: , где - алгебраическая проекция силы на направление, задаваемый ортом . Эта проекция является функцией координаты l и может принимать как положительных так и отрицательных значений.

На «слайде» № 1.6а показано, как элементарная работа δА силы

связана с соответствующим дифференциалом функции скорости . Эта функция получила название кинетической энергии. Обычно в школьных учебниках кинетическую энергию обозначают буквой «Е» с нижним индексом «k» , но мы воспользовались обозначением, которое используется в учебниках общей и теоретической физики.

Обратите внимание на то, что элементарная работа обозначена как δА, хотя

элементарный прирост кинетической энергии записан как dT. Это связано с тем, что в отличие от кинетической энергии Т, которая является функцией скорости, работа А в общем случае не является функцией ни скорости, ни координаты.

Если работа, выполняемая определенной силой над материальной точкой в

процессе ее движения из одной точки пространства в другую, не зависит от траектории этого движения, то такая сила называется потенциальной. В этом случае можно говорить о потенциальной энергии материальной точки, которую она имеет как результат своего положения в определенном месте стационарного (постоянного во времени) силового поля.

Такие силовые поля называют консервативными, поскольку в них

сохраняется сумма потенциальной и кинетической энергии материальной точки (сохраняется полная механическая энергия). На «слайде» № 1.6б рассматриваются три примера потенциальных (консервативных) полей. Правда, как в случае задания № 1, так и в случае задания № 3, говорится о гравитационном поле. Чем эти случаи отличаются, вы должны выяснить самостоятельно (см. задание № 4).

Обратите внимание на то, что потенциальная энергия определяется с точностью до аддитивной константы (вспомните, что первобытные определяются с точностью до аддитивной константы!). Чтобы потенциальная энергия определялась однозначно, обычно договариваются о том, где выбрать точку, в которой потенциальная энергия

будет считаться равной нулю (см. задание № 6).

Результаты, полученные Вами для случая прямолинейного движения материальной точки в поле силы , в дальнейшем будут

обобщены. В конце добавим следующее: по второму закону Ньютона, сила, действующая на тело, равна скорости изменения векторной величины, которую называют импульсом тела (или количеством движения) и обычно обозначают через .

Как это записать формулой? Как найти приращение импульса за время от до , если известна зависимость ?

Дата добавления: 2015-07-11