Анализ экономичности кода

В нашем примере шестибуквенного алфавита равномерный код состоит из трехзначных кодовых обозначений (так как 2² < 6 < 2³ ). На каждую букву в лучшем случае приходится три сигнала. При использовании кода Шеннона-Фано среднее значение числа элементарных сигналов, приходящихся на одну букву сообщения, будет равно (данные берем из таблицы кодирования по методу Шеннона-Фано 8вопрос):

1´0,4 + 2´0,2 + 3´0,2 + 4´0,1 + 5´ (0,05 + 0,05) = 2,3.

Это значительно меньше, чем 3, и не очень далеко от значения энтропии Н: Н = –0,4´ log 0,4 – 2´0,2´ log 0,2 – 0,1´log 0,1 – 2´0,05´log 0,05 = 2,22.

Если провести аналогичный анализ для алфавита, состоящего из 18 букв, то равномерный код будет иметь пятизначное кодовое обозначение, а код Шеннона-Фано будет иметь буквы даже с семью двоичными сигналами, но зато среднее число элементарных сигналов, приходящихся на одну букву, будет равно 3,29 и это немного отличается от величины энтропии Н = 3,25. Особенно выгодно кодировать по методу Шеннона-Фано не отдельные буквы, а сразу целые блоки из нескольких букв. Даже в неблагоприятных случаях кодирование целыми блоками позволяет приближаться к величине энтропии. Рассмотрим пример, когда имеются лишь две буквы А и Б с вероятностями р(А) = 0,7 и р(Б) = 0,3.

Тогда Н = –0,7 log0,7 – 0,3 log0,3 = 0,881.

Применение метода Шеннона-Фано к исходному двухбуквенному алфавиту здесь оказывается бесцельным. Он приводит нас к простейшему равномерному коду, требующему для передачи одного двоичного знака.

Буква	Вероятность	Кодовое обозначение
А Б	0,7 0,3

Здесь мы имеем превышение Н на 12 %. Если применить код Шеннона-Фано к кодированию всевозможных буквенных сочетаний, то

Комбинация букв	Вероятность	Кодовое обозначение
АА АБ БА ББ	0,49 0,21 0,21 0,09

среднее значение длины кодового обозначения в этом случае 1´0,49 + 2´0,21 + 3´0,21 + 3´0,09 = 1,81.

На одну букву приходится 1,81 / 2 = 0,905, что лишь на 3% больше Н = 0,881 бит. При использовании трехбуквенных комбинаций средняя длина кодового обозначения 2,686, то есть на одну букву приходится 0,895 двоичных знаков, что всего на 1,5% больше Н. Рассмотренные примеры анализа степени близости среднего числа двоичных знаков, приходящихся на одну букву сообщения, к значению Н может быть увеличено при помощи перехода к кодированию еще более длинных блоков. Этому обстоятельству посвящена основная теорема кодирования.

Теорема: При кодировании сообщения, разбитого на N –буквенные блоки, можно, выбрав N достаточно большим, добиться того, чтобы среднее число двоичных элементарных сигналов, приходящихся на одну букву исходного сообщения, было сколь угодно близким к Н.

10. Анализ двоичной симметричной линии

Пусть по линии связи передается два элементарных сигнала (А ₁ – импульс, А ₂ – пауза). Вероятность безошибочного приема любого из передаваемых сигналов примем за 1–р, а вероятность ошибки будет равна р. В этом случае р_А1 (А ₁ ) = р_{А 2} (А ₂ ) = 1 –р, а р_{А 1} (А ₂ ) = р_{А 2} (А ₁ ) = р.

Графически схему двоичной симметричной линии принято изображать согласно схеме (рис.13). На рис.13, а отражена конфигурация передаваемого сигнала, а на рис.13,б показано, в какие принимаемые сигналы могут перейти передаваемые сигналы А₁ и А₂ и с какой вероятностью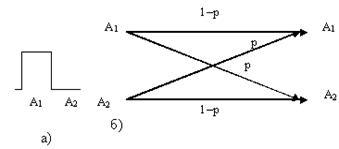

Рис. 13. Схема двоичной симметричной линии: а - характер

сигналов А₁ и А₂; б - схема преобразования сигналов. Для вычисления величины с воспользуемся равенством

I (a, b) = H (b) – H _a (b).

Из схемы (рис.13,б) видно, что если передается сигнал А₁, то на приемном конце с вероятностью 1–р получим тот же сигнал А₁, а с вероятностью р – сигнал А₂. Аналогично с передачей сигнала А₂. Потому

Н_{А 1}(b) = Н_{А 2}(b ) = – (1 –p)log(1 –p) – p log p;

H _a (b) = p (A ₁) H_A1(b) + p(A ₂) H_A2 (b) = – (1– p) log (1– p) – p log p,

так как р(А ₁ ) + р(А ₂ ) = 1.

Отсюда легко сделать вывод о том, что в рассматриваемом случае

H_a ( b ) не зависит от вероятностей р(А₁) и р(А ₂ ), и для вычисления с = max I (a, b) = max [ H (b ) – H _a (b)]надо определить только максимальное значение H (b). Величина H (b) – энтропии опыта b, имеющего только два исхода (рис.13, а) и поэтому она не превосходит одного бита. Значение

H (b ) = 1 достигается при р(А ₁ ) = р(А ₂ ) = 0,5, так как в этом случае оба исхода b будут равновероятными. В рассматриваемом случае р⁰(А₁) = р⁰(А₂) = 0,5,

с = 1 + ( 1 –p) log ( 1 –p) + p log p.

Следовательно, искомая пропускная способность двоичной симметричной линии будет равна

С = L [1 + (1– p) log(1– p) + p log p ].

Последняя формула показывает, как пропускная способность двоичной симметричной линии зависит от вероятности ошибки р.

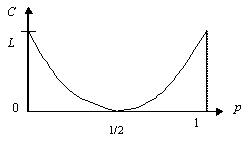Рис. 14. Зависимость пропускной способности двоичной симметричной линии от вероятности ошибки

Наибольшее значение C = L функция достигает при р = 0 (помехи отсутствуют) и р = 1 (А ₁ ® А ₂, А ₂ ® А ₁ ) помеха не мешает понять какой сигнал был передан. При р = 0,5пропускная способность линии равна нулю. Независимо от того, какой сигнал был передан, мы получим на приемном конце с вероятностью 0,5 сигнал А ₁ и с вероятностью 0,5 сигнал А ₂. Принятый сигнал не будет содержать никакой информации.

Вероятность события 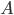равняется отношению числа благоприятствующих исходов к общему числу возможных исходов

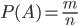(1.1)

где 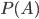— вероятность события 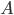, 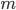— число благоприятствующих событию 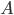исходов, 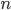— общее число возможных исходов.

Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.

Решение:

А-допущена ошибка в 1

Р(А)=0,4

Р(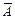)=0,6

В- допущена ошибка во 2

Р(В)=0,4

Р(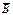)=0,6

С- допущена ошибка в 3

Р(С)=0,4

Р(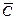)=0,6

Р=

Имеется 5 урн, из которых две содержат по одному белому и по 5 черных шаров, одна урна - 2 белых и 5 черных шаров и последние две урны - по 3 белых и по 5черных шаров. Наудачу выбирается одна урна и из нее наудачу извлекается один шар. Какова вероятность, что этот шар окажется белым?

Решение:

Обозначим через А₁, А₂ и А₃ события, состоящие в том, что шар извлечен из урны, содержащей 1, или 2, или 3 белых шара. В таком случае:

, , .

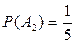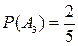Если событие В состоит в том, что извлекается белый шар, то по формуле полной вероятности, получаем:

.

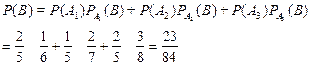Пусть из многолетних наблюдений за погодой известно, что для определенного пункта вероятность того, что 15 июня будет идти дождь, равна 0,4, а вероятность того, что в указанный день дождя не будет, равна 0,6, Пусть далее для этого же пункта вероятность того, что 15 ноября будет идти дождь равна 0,65, вероятность, что будет идти снег - 0,15 и вероятность того, что 15 ноября вовсе не будет осадков равна 0,2. В какой из двух перечисленных дней погоду в рассматриваемом пункте следует считать более неопределенной, если: 1) из всех характеристик погоды интересоваться вопросом о характере осадков; 2) если интересоваться лишь вопросом о наличии осадков.

Решение:

Согласно тому, как понимается здесь слово «погода» имела место 15 июля и 15 ноября, характеризуется следующими таблицами вероятностей:

опыт a₁

исходы опыта	дождь	отсутствие осадков
вероятность	0,4	0,6

опыт a₂

исходы опыта	дождь	снег	Отсутствие осадков
вероятность	0,65	0,15	0,2

1) Поэтому энтропии наших двух опытов равны

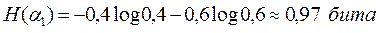
Поэтому погоду 15 ноября в рассматриваемом пункте следует считать более неопределенной, чем 15 июня.

2) Если интересоваться только тем, будут в рассматриваемый день осадки или нет, то исходы «снег» и «дождь» опыта a₂ следует объединить:

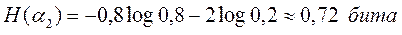Тогда погоду 15 ноября в рассматриваемом пункте следует считать менее неопределенной, чем 15 июня.

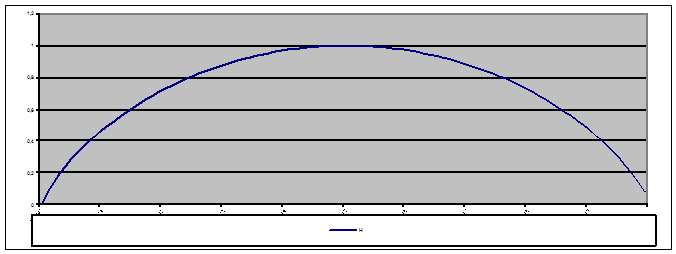
На выходе двоичного источника a информации элементы «0» и «1» появляются с вероятностями соответственно Р и (1-Р). При каком значении Р энтропия источника максимальна? Построить график Н(a) для двоичного источника.

Решение:

1) Строим функциональную зависимость величины энтропии от вероятности Р:

.

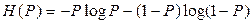Найдем значение Р, при котором данная функция принимает максимальное значение. Для этого ищем экстремум функции: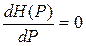

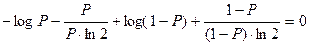
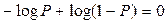
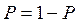, т.о.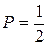

Это подтверждает свойство энтропии, что она максимальна при равновероятных элементах источника.

2) Зная функциональную зависимость 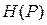получаем следующий график:

Имеются два дискретных троичных источника с независимыми элементами. На выходе каждого источника появляются сообщения одинаковой длины - по 15 элементов. Количество различных элементов в сообщении каждого источника постоянно. Сообщения каждого источника отличаются только порядком элементов. Зафиксированы два типичных сообщения: 021202120212021 - первого источника и 012101201101201 - второго. Появление элемента какого источника в среднем наиболее неопределенно?

Дата добавления: 2015-10-21