Теорема 1.

Теория квадратичных вычетов

Рассмотрим сравнение xⁿ ≡ a (mod m) *, (a, m)=1. Если * имеет решение, то а называется вычетом степени n по модулю m. Если n =2, то вычеты называются квадратичными, если n =3 – кубическими, n =4 – биквадратичными. Если * решений не имеет, то а называется невычетом степени n по модулю m.

Далее будем рассматривать случай n =2, т.е. сравнения вида x ²≡ a (mod m), (a, m)=1.

Квадратичные вычеты по простому модулю.

В этом пункте будем рассматривать сравнения вида x ²≡ a (mod p), p >2 – простое число.

Теорема 1.

Если а – квадратичный вычет по простому модулю р, то сравнение x ²≡ a (mod p) имеет ровно 2 решения.

Доказательство:

Если а – квадратичный вычет по модулю p, то найдется хотя бы одно решение исходного сравнения: x≡x ₁(mod p).

Но, поскольку (— x ₁)²= x ₁², то решением также является x≡—x ₁(mod p), причем x ₁ —x ₁(mod p), т.к. р – нечетное число.

Более двух решений данное сравнение иметь не может, так как является сравнением второй степени (§4, п.3, Теорема 2).

□

Теорема (о числе квадратичных вычетов)

Приведенная система вычетов по модулю p состоит из квадратичных вычетов и квадратичных невычетов.

Доказательство:

Среди вычетов приведенной системы по модулю p квадратичными вычетами являются только те, что сравнимы с квадратами чисел

…, –2, –1, 1, 2,…, , т.е. с числами 1, 2², 3²,…,

При этом квадраты не сравнимы между собой по модулю p, т.к. иначе из того, что k ² ≡ l ² (mod p), 0 < k < l следовало бы, что сравнению x ²≡ l ²(mod p) удовлетворяют 4 числа: – l, l,– k, k, что противоречит Теореме 1.

Таким образом, квадратичных вычетов в приведенной системе по модулю p ровно штук. Остальные элементы приведенной системы являются квадратичными невычетами. А поскольку всего в приведенной системе по модулю p содержится p— 1 элементов, то квадратичными невычетами являются также элементов.

□

Множество квадратных вычетов по модулю p обозначается Q (p), множество квадратичных невычетов – .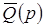

Дата добавления: 2015-09-07