Методы анализа устойчивости социально-технических систем

Анализ характера динамических процессов (в частности, устойчивости), протекающих в сложных системах под действием возмущений различной природы, является важнейшим звеном формальных процедур решения широкого класса задач управления. Характерными задачами этого типа являются: выработка стратегии региональной эко­логической политики, выбор и исследование эффективности экономических и правовых механизмов регулирования техногенного и природного риска, прогно­зирование тенденций в общественно-политических процессах и ряд других. Для большинства практических приложений указанного класса задач харак­терен низкий уровень точности исходных данных и качественный характер описания ряда зависимостей, что делает бессмысленным стремление к получению строгих количественных решений на точных количественных моделях.

В этих условиях повышается роль методов анализа, позволяющих делать суждения о динамических процессах и устойчивости по информации о струк­турных особенностях исследуемой системы. Анализ использования различных математических моделей применительно к оценке развития и функционированию социально экономических систем показывает, что для этих целей достаточно удобно использовать аппарат знаковых, взвешенных знаковых и функциональных знаковых графов. Аппарат позволяет работать с данными как качественного, так и количественного типа, причем степень использования количественных данных может увеличиваться в зависимости от возможностей количественной оценки взаимодействующих факторов в итерационном цикле моделирования.

Аппарат знаковых графов позволяет формально строить сценарии развития или траектории движения моделируемой системы в фазовом пространстве ее переменных на основе информации о ее структуре и программах развития системы.

Математическая модель знаковых, взвешенных знаковых, функциональных знаковых графов является расширением математической модели графов. Кроме графа G(X,Е) в модель включаются следующие компоненты.

1. Множество параметров вершин V. Каждой вершине 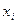ставится в соответствие её параметр .

2. Функционал преобразования дуг F(V,E), ставящий соответствие каждой дуге либо знак, либо вес, либо функцию.

Если функционал имеет вид

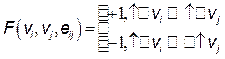
то такая модель называется знаковым графом.

Если функционал имеет вид

то такая модель называется взвешенным знаковым графом. Здесь 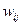является весом соответствующей дуги.

Если функционал имеет вид

то такая модель называется функциональным знаковым орграфом.

Импульсом в вершине x_i, в момент времени n называется изменение параметра в этой вершине в момент времени n.

Используются понятия четного и нечетного циклов. Четный цикл имеет поло­жительное произведение знаков всех входящих в него дуг, нечетный — отрицательное.

Четный цикл является простейшей моделью структурной неустойчивости, так как любое начальное изменение параметра в любой его вершине приводит к неограниченному росту модуля параметров вершин цикла, в то время как любое начальное изменение параметра любой вершины нечетного цикла приведет лишь к осцилляции (колебанию) параметров вершин.

Вершина знакового, взвешенного знакового, функционального знакового графа является импульсно устойчивой для некоторого заданного импульсного процесса, если последовательность абсолютных величин импульсов в этой вершине ограничена.

Далее, вершина x_i знакового (и др.) графа является абсолютно устойчивой для некоторого заданного импульсного процесса, если последовательность абсолютных величин параметров в этой вер­шине ограничена.

Знаковый (и др.) орграф называется импульсно (абсолютно) устойчивым для данного импульсного процесса, если каждая его вершина является импульсно (абсолютно) устойчивой в этом импульсном процессе.

Утверждение 1. Знаковый граф, не содержащий циклов, импульсно устой­чив для всех простых импульсных процессов. Кроме того, для любого импульс­ного процесса существует конечный момент времени, после которого импульсы во всех вершинах в любой последующий момент равны 0.

Утверждение 2. Знаковый граф, содержащий лишь один цикл, импульсно устойчив для всех простых импульсных процессов.

Утверждение 3. Знаковый граф, содержащий только невзаимодействующие между собой циклы, импульсно устойчив во всех простых импульсных процессах.

Из утверждений 1, 2, 3 и следует, что резонанс - единственная причина импульсной неустойчивости в автономных импульсных процессах.

Для анализа графа важным является проверка его как на абсолютную устойчивость (устойчивость по значениям вершин), так и на импульсную устойчивость. При наличии неустойчивости графа в описываемой им системе могут происходить нежелательные процессы.

Граф считается абсолютно или импульсно устойчивым в импульсном процессе при устойчивости каждой его вершины. При анализе знакового графа на устойчивость можно использовать собственные значения его матрицы смежности и ряд необходимых в этом случае теорем.

Теорема 1. Если взвешенный граф импульсно устойчив для всех простых импульсных процессов, то каждое собственное значение его матрицы смежности по абсолютной величине не превосходит единицу.

Теорема 2. Если все ненулевые собственные значения матрицы смежности взвешенного графа различны и не превосходят по абсолютной величине единицы, то это граф импульсно устойчив для всех простых импульсных процессов.

Теорема 3. Взвешенный граф абсолютно устойчив для любого простого импульсного процесса тогда и только тогда, когда этот граф импульсно устойчив для любого простого импульсного процесса и среди собственных значений его матрицы смежности нет ни одного равного единице.

Подобрать значения графа так чтобы он был импульсно устойчив, чрезвычайно затруднительно даже опытному эксперту, поскольку о механизме воздействия структуры на устойчивость известно совсем немного.

Для анализа знакового орграфа на устойчивость находятся собственные значения l _i матрицы A, путем решения ее характеристического уравнения det(A – lE)=0, где l — собственный вектор A; E — единичная матрица (см. сноску).

Возможные стратегии улучшения импульсной и абсолютной устойчивости могут быть следующими.

1. Изменение в некоторый момент времени значений отдельных вершин.

2. Добавление в любое время новой вершины (фактора).

3. Изменение знаков некоторых дуг.

4. Добавление новых дуг между имеющимися вершинами ориентированного графа.

5. Введение новых контуров (положительной или отрицательной обратной связи).

6. Исключение некоторых контуров.

В случае, когда допустимое множество стратегий определено, можно потребовать найти среди них оптимальную (например, самую дешевую) для обеспечения устойчивости системы.

Таким образом, применение аппарата знаковых графов для исследования эффективности и устойчивости функционирования систем позволяет получить достаточно точные предварительные прогнозы. Это позволит выявить «узкие места» исследуемой системы или неточности в описании исходных данных.

Для матрицы А размерностью n² любой вектор X ÎVⁿ (Vⁿ — векторное пространство размерностью n), X ¹0, для которого выполняется равенство AX = lX, где l — некоторое число, называется собственным вектором А, а l — собственным значением матрицы А. Поскольку AX = lX Þ (А – lE) X =0 — система линейных уравнений, решение которой является искомыми собственными векторами. Уравнение (А – lE) X =0 имеет решение тогда и только тогда, если det(А – lE) X =0 (характеристическое уравнение матрицы А).

Литература к задаче 5

Робертс Ф. С. Дискретные математические модели с приложениями к социальным, биологическим и экологическим задачам: Пер. с англ. – М.: Наука. Гл. ред. физ.-мат. лит., 1986, – 496 с.

Дата добавления: 2015-10-13