Теорема Максвелла—Мора.

Прогиб балки в точке приложения сосредоточенной силы Р равен:

аналогичное выражение мы имеем и для угла поворота с заменой производной на . Выясним, что представляют собой эти производные.

Если на балке расположена какая угодно нагрузка из сосредоточенных сил 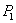, , 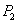,..., моментов , ,..., сплошных нагрузок , ..... то момент М(х) в любом сечении такой балки выражается линейной функцией от нагрузок:

Рис.2. Частная расчетная модель метода Максвелла — Мора.

Коэффициенты 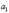, ,..., , 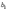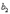…, , ... являются функциями пролета балки, расстояний точек приложения сил и моментов от опор и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки приложения силы ; тогда

так как , ,..., , 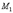,..., , ..., , ,..., , …, , ... при этом дифференцировании постоянны. Но можно рассматривать как численную величину момента М в любом сечении балки от действия так называемой единичной нагрузки, т. е. силы ; действительно, подставляя в формулу вместо его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем .

Например, для балки, изображенной на Рис2, а, изгибающий момент равен:

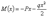
Производная 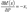; но это как раз и будет выражение изгибающего момента нашей балки, если мы ее нагрузим силой 1, приложенной в той же точке В, где расположена сила Р (Рис.2, б), и направленной в ту же сторону.

Аналогично, производная изгибающего момента М (х) по паре сил 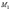численно представляет собой изгибающий момент от пары с моментом, равным единице, приложенной в том же сечении, где имеется пара , и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой .

Таким образом, для отыскания перемещения (прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента от соответствующей единичной нагрузки, приложенной в сечении, где ищем перемещение ; тогда это перемещение выразится формулой

Эта формула была предложена Максвеллом в 1864 г. и введена в практику расчета О. Мором в 1874 г. Если мы в полученном выражении под подразумеваем прогиб, то момент надо вычислять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице.

Для примера рис.2 имеем:

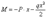
	(рис.2,а)
	(рис.2, б)

Знак плюс означает, что направление перемещения совпадает с направлением единичной нагрузки, знак минус — наоборот.

Если при определении изгибающих моментов придется делить балку на участки, то соответственно и интеграл в формуле распадется на сумму интегралов.

Сравнивая формулу Кастильяно с формулой Мора, нетрудно заметить, что они отличаются лишь одним множителем. В теореме Кастильяно или , в теореме Мора .

Следовательно, производная от изгибающего момента по обобщенной силе — это то же самое, что изгибающий момент от силы .

5. Профессором Когаевым В.П.и академиком Серенсеном С.В. разработана теория подобия усталостного разрушения, которая позволяет расчетным методом определить совместное влияние концентрации напряжений и масштабного эффекта, как отношение предела выносливости лабораторного образца s _-1 к пределу выносливости детали s _-1д при симметричном цикле изменения напряжений из следующего уравнения:

где 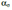- теоретический коэффициент концентрации для первого главного напряжения в зоне концентрации рассчитываемой детали; L - часть периметра опасного поперечного сечения детали, в котором действуют максимальные напряжения; G - относительный максимальный градиент первого главного напряжения в зоне концентрации детали; GL /lg - параметр подобия детали; _- справочная характеристика материала детали, ориентировочные значения которой приведены ниже для некоторых сплавов:

= 0,1-0,18 – для углеродистых сталей;

= 0,04-0,12 – для легированных сталей;

= 0,09-0,2 – для алюминиевых сплавов.

Дата добавления: 2015-08-21