Общий случай задачи оптимизации

Обозначим х₁=а, x₂=b, x₃=h, тогда запишем:

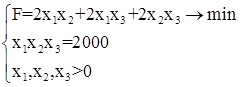(7.6)

Очевидно, что (7.6) можно записать:

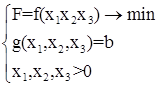(7.7)

Тогда в общем случае можно записать так:

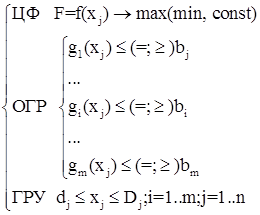(7.8)

Систему (7.8) принято записывать более компактно:

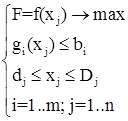(7.9)

Запись (7.9) является общей формой записи задач оптимизации. В эту систему входят три составляющие:

1. ЦФ – целевая функция или критерий оптимизации, показывает, в каком смысле решение должно быть оптимальным, т.е. наилучшим. При этом возможны 3 вида назначения целевой функции:

r Максимизация.

r Минимизация.

r Назначение заданного значения.

2. ОГР – ограничение, устанавливают зависимости между переменными. Они могут быть односторонними: g_i(x_j)£b_i, или двухсторонними: a_i£g_i(x_i)£b_i. Причем любое двусторонне ограничение можно записать в виде двух односторонних: g_i(x_j)³a_i, g_i(x_j)£b_i .

3. ГРУ – граничные условия. Показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

Решения задачи, удовлетворяющие всем ограничениям и граничным условиям, называются допустимыми. Если математическая модель составлена правильно, то мы будем иметь целый ряд допустимых решений.

Важной характеристикой задачи оптимизации является ее размерность, определяемая числом переменных n и числом ограничений m. Соотношение этих величин является определяющим при постановке задачи оптимизации. Возможны три соотношения n<m, n=m, n>m.

1. n<m
например:

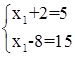
Здесь n=1, m=2. Очевидно, что такие задачи решения не имеют, за исключением случая линейно зависимой системы уравнений:
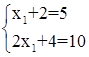(то же что случай 2, при n=m=1)

2. n=m

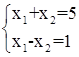
Здесь n=m=2. Существует единственное решение, за исключением случая линейно зависимой системы уравнений:
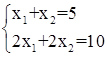(то же, что случай 3, при n=2, m=1)

3. n>m
x₁+x₂=5
Здесь n=2, m=1. Существует бесконечное множество решений.

Так как большинство ограничений записываются в виде неравенств, то рассмотрим, например, следующее неравенство:

х₁£5.

Введем дополнительную переменную y₁³0 и перейдем от заданного неравенства к уравнению:

x₁+y₁=5

Для этого уравнения n=2, m=1, и следовательно оно имеет бесконечное множество решений.

В общем случае ОГР имеют вид:

g_i(x_j)£b_i

i=1..m; j=1..n;

то их можно записать в виде:

g_i(x_j)+y_i=b_i

y_i³0; i=1..m; j=1..n.

В этом случае общее число переменных x_j и y_i , равное N будет: N=n+m, а число уравнений останется прежним равным m.

Очевидно, что N=n+m>m, и система имеет бесчисленное множество решений. Значит, если ограничениями являются неравенства, то система всегда имеет бесчисленное множество решений.

Т.о. условие n>m – это непременное требование задач оптимизации.

Оптимальное решение – (optimus от лат. наилучший) это наилучшее решение, но наилучшего решения во всех смыслах быть не может. Может быть лучшим только в одном, строго установленном смысле.

Принимающий решение должен абсолютно точно представлять, в чем заключается оптимальность решения, т.е. по какому критерию (kriterio – мерило, оценка) принимаемое решение должно быть оптимальным.

Критерий называют целевой функцией (ЦФ). С помощью критерия можно оценивать качества как желательные (например прибыль, производительность, надежность), так и нежелательные (затраты, расходы, простои и т.д.). Тогда в первом случае стремятся к максимизации критерия, во втором – к минимизации.

Итак, задача имеет оптимальное решение, если она удовлетворяет двум требованиям:

r есть реальная возможность иметь более одного решения, т.е. существуют допустимые решения;

r имеется критерий, показывающий, в каком смысле принимаемое решение должно быть оптимальным, т.е. наилучшим из допустимых.

Дата добавления: 2015-10-31