Схема интегрирования рациональной дроби

Вычисление интеграла

(8.1)

от рациональной дроби ( – многочлены степеней соответственно) сводится к следующему:

1) проверяют, является ли рациональная функция правильной рациональной дробью (). Если она не является таковой (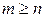), то сначала необходимо разделить столбиком многочлен на многочлен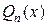

,

в результате чего выделятся неполное частное , являющееся многочленом степени , и рациональная функция , являющаяся правильной рациональной дробью ();

2) раскладывают исходную рациональную дробь 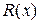(если она являлась правильной) или полученную правильную рациональную дробь (если 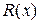являлась неправильной) на сумму простейших дробей. При этом необходимо определить все коэффициенты разложения (см. ниже);

3) вычисляют интегралы от многочлена (интегралы от степенных функций), а также интегралы от простейших дробей.

Пример 1. Вычислить интеграл .

Решение: Заметим, что подынтегральная функция является правильной рациональной дробью. Поэтому разложим ее на сумму простейших дробей. Исходное разложение имеет вид

. (8.2)

Найдем коэффициенты по методу неопределенных коэффициентов. Для этого правую часть равенства (6.2) приведем к общему знаменателю:

Приравняем числитель полученной дроби к числителю 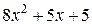исходной функции , то есть

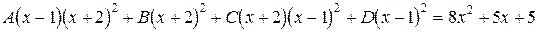. (8.3)

Из полученного равенства (6.3) и найдем неизвестные коэффициенты . Существуют два способа нахождения этих коэффициентов: способ сравнения коэффициентов и способ частных значений (эти два метода равносильны, а их использование зависит от конкретной задачи).

Поясним смысл способа сравнения коэффициентов. Раскрыв левую часть равенства (6.3), выделим коэффициенты при одинаковых степенях :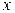

.

Полученный многочлен (с неизвестными коэффициентами) должен по условию равняться многочлену 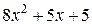, а два многочлена равны только в том случае, когда равны коэффициенты при соответственных степенях переменной 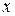. В результате получаем систему

Решив эту систему методом Гаусса, получим .

Удобно здесь применить способ частных значений, состоящий в том, что в левую и правую части равенства (8.3) подставляют какие-то частные (удобные) значения аргумента 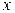(такими являются часто корни знаменателя или еще какие-то значения). Тогда задача нахождения неизвестные коэффициентов значительно упрощается. В данном случае в равенство (8.3) удобно подставить значения 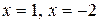(корни знаменателя функции ), . Получим (см. равенство (8.3))

,

,

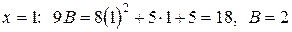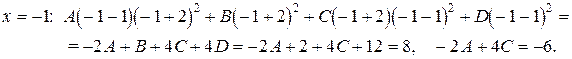
Легко и в этом случае найти коэффициенты .

Итак, найдя коэффициенты , разложение (8.2) примет вид

Окончательно вычисляем интеграл =

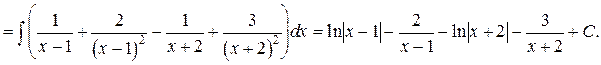
Пример 2. Вычислить интеграл .

Решение: В примере подынтегральная функция не является правильной рациональной дробью (, ). Используя метод выделения целой части (многочлена), получим

.

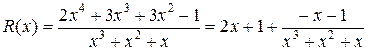Теперь необходимо правильную рациональную дробь = 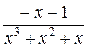разложить на простейшие дроби. Соответствующее разложение будет иметь следующий вид

= (8.4)

Найдем коэффициенты 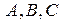по методу неопределенных коэффициентов (методом сравнения коэффициентов). Для этого приведем правую часть равенства (8.4) к общему знаменателю

,

откуда получим равенство 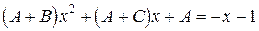для нахождения коэффициентов 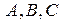. Переходя от последнего равенства к системе (приравняв коэффициенты при одинаковых степенях аргумента )

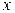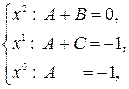
найдем .

Итак, имеем окончательно, Теперь не вызывает трудности вычислить исходный интеграл от функции :

Лекция 6

Дата добавления: 2015-10-30