
Читайте также:
|
Металлургический факультет
Кафедра высшей математики
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Индивидуальные задания
Новокузнецк 2005
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Сибирский государственный индустриальный университет»
Кафедра высшей математики
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Индивидуальные задания
Новокузнецк 2005
УДК 519.075
Рецензент
доктор физико-математических наук,
профессор, заведующий кафедрой физики СибГИУ
В.Е.Громов
Неопределенный интеграл: индивидуальные задания / Сост.: М.С.Волошина, С.Ф.Гаврикова, О.В.Олесюк: СибГИУ. – Новокузнецк, 2005. – 16 с.
Даны 25 вариантов индивидуальных заданий по теме «Неопределенный интеграл». Приведены образец решения типового варианта и таблица основных неопределенных интегралов.
Предназначены для студентов всех специальностей.
Варианты индивидуальных заданий
Вариант № 1
1)  ; 6)
; 6)  ; 11)
; 11) 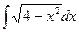 ;
;
2)  ; 7)
; 7)  ; 12)
; 12) 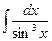 ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 2
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3) 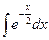 ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 3
1)  ; 6)
; 6) 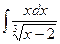 ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12) 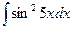 ;
;
3)  ; 8)
; 8) 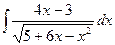 ; 13)
; 13)  ;
;
4) 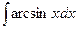 ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10) 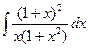 ; 15)
; 15)  .
.
Вариант № 4
1)  ; 6)
; 6)  ; 11)
; 11) 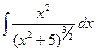 ;
;
2)  ; 7)
; 7) 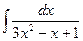 ; 12)
; 12) 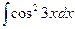 ;
;
3) 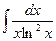 ; 8)
; 8)  ; 13)
; 13) 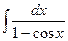 ;
;
4)  ; 9)
; 9)  ; 14)
; 14) 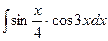 ;
;
5) 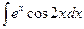 ; 10)
; 10) 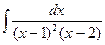 ; 15)
; 15)  .
.
Вариант № 5
1)  ; 6)
; 6) 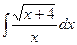 ; 11)
; 11)  ;
;
2)  ; 7)
; 7) 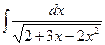 ; 12)
; 12)  ;
;
3) 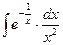 ; 8)
; 8)  ; 13)
; 13) 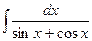 ;
;
4)  ; 9)
; 9)  ; 14)
; 14) 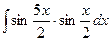 ;
;
5) 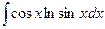 ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 6
1)  ; 6)
; 6)  ; 11)
; 11) 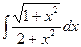 ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14) 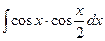 ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 7
1) 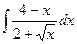 ; 6)
; 6) 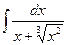 ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9) 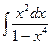 ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 8
1) 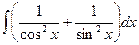 ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7) 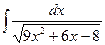 ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10) 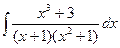 ; 15)
; 15)  .
.
Вариант № 9
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2) 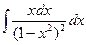 ; 7)
; 7) 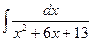 ; 12)
; 12)  ;
;
3) 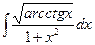 ; 8)
; 8)  ; 13)
; 13) 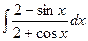 ;
;
4)  ; 9)
; 9) 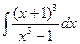 ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 10
1)  ; 6)
; 6) 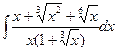 ; 11)
; 11)  ;
;
2) 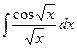 ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 11
1)  ; 6)
; 6) 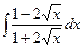 ; 11)
; 11) 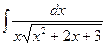 ;
;
2)  ; 7)
; 7)  ; 12)
; 12) 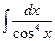 ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15) 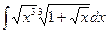
Вариант № 12
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2) 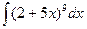 ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13) 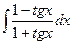 ;
;
4) 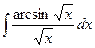 ; 9)
; 9)  ; 14)
; 14) 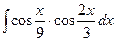 ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 13
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12) 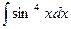 ;
;
3)  ; 8)
; 8)  ; 13)
; 13) 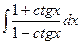 ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5) 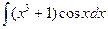 ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 14
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13) 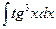 ;
;
4)  ; 9)
; 9)  ; 14)
; 14) 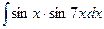 ;
;
5) 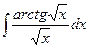 ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 15
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4) 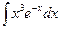 ; 9)
; 9)  ; 14)
; 14) 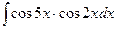 ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 16
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2) 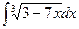 ; 7)
; 7)  ; 12)
; 12)  ;
;
3) 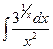 ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14) 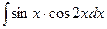 ;
;
5) 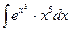 ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 17
1) 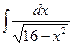 ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7) 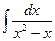 ; 12)
; 12)  ;
;
3)  ; 8)
; 8) 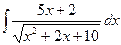 ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10) 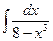 ; 15)
; 15)  .
.
Вариант № 18
1)  ; 6)
; 6) 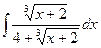 ; 11)
; 11)  ;
;
2)  ; 7)
; 7) 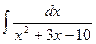 ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13) 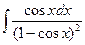 ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15) 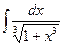 .
.
Вариант № 19
1) 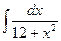 ; 6)
; 6)  ; 11)
; 11)  ;
;
2) 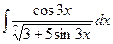 ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4) 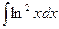 ; 9)
; 9) 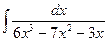 ; 14)
; 14) 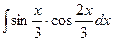 ;
;
5)  ; 10)
; 10)  ; 15)
; 15) 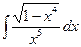 .
.
Вариант № 20
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13) 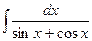 ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 21
1) 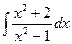 ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7) 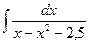 ; 12)
; 12)  ;
;
3)  ; 8)
; 8) 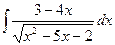 ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 22
1) 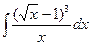 ; 6)
; 6) 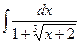 ; 11)
; 11)  ;
;
2) 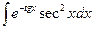 ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8)  ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 23
1) 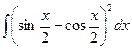 ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3) 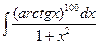 ; 8)
; 8) 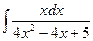 ; 13)
; 13)  ;
;
4) 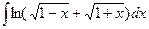 ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 24
1)  ; 6)
; 6) 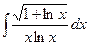 ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3)  ; 8)
; 8) 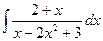 ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Вариант № 25
1)  ; 6)
; 6)  ; 11)
; 11)  ;
;
2)  ; 7)
; 7)  ; 12)
; 12)  ;
;
3) 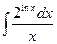 ; 8)
; 8) 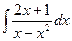 ; 13)
; 13)  ;
;
4)  ; 9)
; 9)  ; 14)
; 14)  ;
;
5)  ; 10)
; 10)  ; 15)
; 15)  .
.
Таблица основных неопределенных интегралов
1. 
2. 
3. 
4. 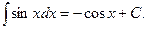
5. 
6. 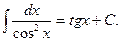
7. 
8. 
9. 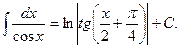
10. 
11. 
12. 
13. 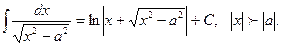
14. 
15. 
16. 
17.  18.
18. 
Свойства неопределенного интеграла
1. 
2. 
3. 
4. 
Образец решения типового варианта индивидуального задания
Задание 1. Тема: интегрирование по таблице. Вычислить интеграл  .
.
Решение. Используем метод непосредственного интегрирования. Применив свойства 3 и 4, имеем

Далее, используя соответственно формулы 4, 1, 1, 2, 10 таблицы основных интегралов, находим:

Задание 2. Тема: подведение переменной под знак дифференциала. Вычислить интеграл  .
.
Решение. Принимая во внимание, что  , и применяя формулу 1 таблицы основных интегралов, получаем:
, и применяя формулу 1 таблицы основных интегралов, получаем:
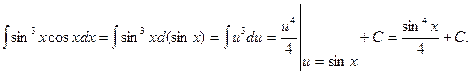
Задание 3. Тема: подведение переменной под знак дифференциала. Вычислить интеграл  .
.
Решение. Учитывая, что 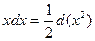 , и применяя формулу 14 (где
, и применяя формулу 14 (где 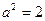 ), основной таблицы интегралов, имеем:
), основной таблицы интегралов, имеем:

Задание 4. Тема: интегрирование по частям. Вычислить интеграл  .
.
Решение. Используем формулу интегрирования по частям 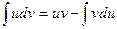 .
.
Полагаем 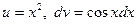 . Тогда
. Тогда  . Применяя формулу, получаем:
. Применяя формулу, получаем:
 .
.
К стоящему справа интегралу снова применяем формулу интегрирования по частям, причем полагаем  . Отсюда
. Отсюда 
Применяя формулу интегрирования по частям, получаем окончательно:
 .
.
Задание 5. Тема: интегрирование по частям. Вычислить интеграл  .
.
Решение. Для применения формулы интегрирования по частям  полагаем
полагаем  . Тогда
. Тогда  и
и
 .
.
Теперь полагаем  . Тогда
. Тогда  и
и
 .
.
В итоге получено уравнение относительно неизвестного интеграла  . Решая это уравнение, находим:
. Решая это уравнение, находим:
 ,
,
или 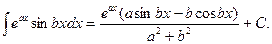
Задание 6. Тема: интегрирование подстановкой (заменой переменной). Вычислить интеграл  .
.
Решение. Сделаем замену переменной по формуле  , тогда
, тогда  , откуда
, откуда


Задание 7. Тема: интегрирование выражений, содержащих квадратный трехчлен в знаменателе. Вычислить интеграл 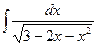 .
.
Решение. Выделим полный квадрат в многочлене, стоящем под знаком корня:
 .
.
Тогда, подводя переменную  под знак дифференциала и применяя формулу 12 (при
под знак дифференциала и применяя формулу 12 (при  ) таблицы основных интегралов, получим:
) таблицы основных интегралов, получим:
 .
.
Задание 8. Тема: интегрирование выражений, содержащих квадратный трехчлен в знаменателе. Вычислить интеграл  .
.
Решение. Выделив в числителе производную знаменателя, поделив почленно числитель на знаменатель и затем применив для каждого из двух полученных интегралов соответственно формулы 2 и 10 таблицы основных интегралов, имеем:


Задание 9. Тема: интегрирование рациональных дробей методом неопределенных коэффициентов. Вычислить интеграл  .
.
Решение. Дробь  - правильная, ее разложение в сумму простейших дробей имеет вид:
- правильная, ее разложение в сумму простейших дробей имеет вид:

Приводя правую часть к общему знаменателю, получаем
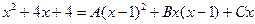
(тождественное равенство числителей), откуда, приравнивая коэффициенты при одинаковых степенях х, имеем
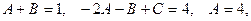
и далее находим

Следовательно,

Задание 10. Тема: интегрирование рациональных дробей методом неопределенных коэффициентов. Вычислить интеграл 
Решение. Дробь  - правильная, ее разложение в сумму простейших дробей имеет вид
- правильная, ее разложение в сумму простейших дробей имеет вид
 .
.
Имеем
 .
.
Полагая  , находим
, находим  Приравнивая коэффициенты при одинаковых степенях х, получаем
Приравнивая коэффициенты при одинаковых степенях х, получаем  т.е.
т.е.
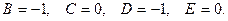
Следовательно,

Задание 11. Тема: интегрирование иррациональных функций с помощью тригонометрических подстановок. Вычислить интеграл  .
.
Решение. Выделяя полный квадрат в квадратном трехчлене, имеем:
 , где
, где  .
.
Производя теперь подстановку  получаем:
получаем:
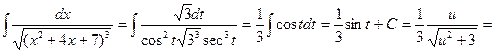

Задание 12. Тема: интегрирование тригонометрических функций. Вычислить интеграл 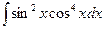 .
.
Решение. Применяя формулы понижения степени  имеем:
имеем:


Задание 13. Тема: интегрирование тригонометрических функций. Вычислить интеграл 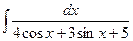 .
.
Решение. Применим универсальную тригонометрическую подстановку. Полагаем  , тогда
, тогда  и
и


Задание 14. Тема: интегрирование произведений синусов и косинусов различных аргументов. Вычислить интеграл  .
.
Решение. Для вычисления интеграла подобного типа используется одна из формул
 ,
,
 ,
,
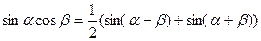 .
.
Имеем

Задание 15. Тема: интегрирование дифференциальных биномов. Вычислить интеграл  .
.
Решение. Интеграл от дифференциального бинома  , если
, если  - рациональные числа, приводится к интегралу от рациональной функции и, следовательно, выражается через элементарные функции в следующих трех случаях:
- рациональные числа, приводится к интегралу от рациональной функции и, следовательно, выражается через элементарные функции в следующих трех случаях:
1) 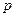 есть целое число (подстановка
есть целое число (подстановка  , где
, где  - наименьшее общее кратное знаменателей дробей
- наименьшее общее кратное знаменателей дробей  и
и  );
);
2) 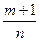 есть целое число (подстановка
есть целое число (подстановка  , где
, где  - знаменатель дроби
- знаменатель дроби 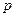 );
);
3)  есть целое число (подстановка
есть целое число (подстановка 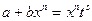 , где
, где  - знаменатель дроби
- знаменатель дроби 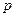 ).
).
Запишем данный дифференциальный бином в стандартном виде:
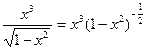 .
.
Здесь  - целое число.
- целое число.
Делаем замену  ,тогда
,тогда  и
и
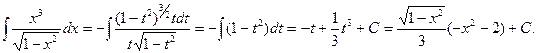
СПИСОК ЛИТЕРАТУРЫ
1. Пискунов Н.С. Дифференциальное и интегральное исчисления, т. 1.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление.
3. Письменный Д.Т. Конспект лекций по высшей математике, т. 1.
4. Ефимов А.В. Сборник задач по математике для втузов, т. 1.
5. Шипачев В.С. Задачник по высшей математике.
Составители:
Волошина Марина Сергеевна
Гаврикова Светлана Федоровна
Олесюк Ольга Васильевна
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Индивидуальные задания
Напечатано в полном соответствии с авторским оригиналом
Изд. лиц. № 01439 от 05.04.2000 г. Подписано в печать г.
Формат бумаги 60х84 1/16. Бумага писчая. Ризография.
Усл. печ. л.. Уч.-изд. л.. Тираж 100 экз. Заказ.
Сибирский государственный индустриальный университет
654007, г. Новокузнецк, ул. Кирова, 42.
Издательский центр СибГИУ
Дата добавления: 2015-10-30; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование рациональных функций | | | ДЕ 1. Неопределенный интеграл |