Упражнения и задачи. Представить в тригонометрической форме:

Представить в тригонометрической форме:

а) -2; б) i; в) -2 i; г) д) 4-3 i; е)

Представить в алгебраической форме:

а) б)

Выполнить умножение:

а)

б)

Представить в тригонометрическом виде:

а) б)

Формула Муавра

Если 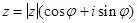– тригонометрическая форма записи комплексного числа z, то

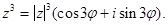
Для любой натуральной степени числа z по индукции получим:

Заметим, если то и

Для натурального числа п получим:

т.е. для любого целого числа п имеет место равенство (формула Муавра):

Пример. Доказать, что

Решение: По формуле Муавра:

С другой стороны, по формуле сокращенного умножения:

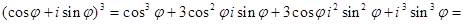
Отсюда

Тогда

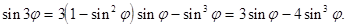
Пример. Найти сумму

Решение: Рассмотрим суммы:

Тогда

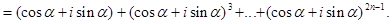
Применяя формулу суммы членов геометрической прогрессии, получим:

Итак,

Пример. Найти сумму: а) б) .

Решение: По формуле бинома Ньютона имеем:

По формуле Муавра находим:

Приравнивая вещественные и мнимые части полученных выражений для , имеем

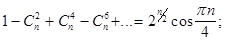
Пример. Выразить через тригонометрические функции кратных углов.

Решение: Пусть Тогда и

Упражнения и задачи

Выразить через и :

а) б) в) г) д)

Выразить через тригонометрические функции кратных углов:

а) б) в)

Вычислить суммы:

а) б)

в) г)

Вычислить: а) б) в)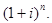

Доказать, что если

Модуль комплексного числа

Напомним некоторые свойства модуля комплексного числа:

если

Теорема: (Неравенство треугольника: сумма двух сторон треугольника не меньше его третьей стороны).

Доказательство: Тогда Отсюда т.е. ■

Пример. Доказать, что

Доказательство: 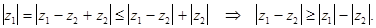Аналогично,

Пример. a,b – комплексные числа. Если – вещественное положительное число, то Доказать это.

Доказательство:

Упражнения и задачи

При каком условии точка 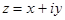лежит внутри круга радиуса R и центром в точке

Доказать равенства:

а)

б)

Доказать, что если то

Доказать, что уравнения с вещественными коэффициентами

не могут иметь корней, больше единицы по модулю.

Решить уравнение:

а) б)

Дата добавления: 2015-10-23