Порядок виконання роботи. 1. Побудуйте фазовий портрет вільного руху системи оптимального керування для

1. Побудуйте фазовий портрет вільного руху системи оптимального керування для власного типу нелінійності (на рис. 15 НЭ), взятого з таблиці 3.1. Варіант завдання вибирати відповідно до списку у журналі академгрупи. Проаналізуйте лінії перемикання і їх положення на фазовій площині залежно від значення коефіцієнта k.

Таблиця 3.1

Параметри реле

Тип реле	m	b	- b	c	- c
Трипозиційне без гістерезису			-1		-1
	0,35	-0,35		-2
	8,3	-8,3		-12
	15,5	-15,5		-27
Трипозиційне з гістерезисом	0,5		-1		-2
0,23		-5	1,5	-1,5
0,7		-4		-12
0,05		-24		-21
Двопозиційне без гістерезису
				-8
			4,3	-4,3
				-15
Двопозиційне з гістерезисом	-1	0,5	-4,5		-3
-1		-6	4,5	-4,5
-1	8,5	-12,5		-13
-1		-17		-21

m – коефіцієнт, що приймає значення з інтервалу (-1,1), параметри нелінійних елементів с, - с, b, - b наведено на рисунку 12.

2. Вивчить шляхом цифрового моделювання оптимальні процеси при k = const, x₁⁰ = var, x₂⁰ = var. Зафіксуйте оптимальні фазові траєкторії та відповідні їм процеси x ₁(t), x ₂(t), u (t), а також значення функціоналів якості J ₁, J ₂ і J.

3. Дослідіть залежність функціоналів якості J ₁ і J ₂ від значення вагового коефіцієнта k. Для цього при тих самих початкових умовах, x ₁= const x ₂⁰=0 проведіть обчислювальні експерименти з різними k і побудуйте крапки залежностей J ₁(k) і J₂ (k). Сформулюйте методичні рекомендації з вибору коефіцієнта k, виходячи з компромісних вимог до швидкодії та втрат на керування.

Зміст звіту

Звіт повинен містити: постановку завдання; структурну схему системи оптимального керування; фазовий портрет вільного руху, оптимальні фазові траєкторії та процеси, чисельне значення функціоналів якості; експериментальні залежності J ₁(k) і J ₂(k); висновки.

Контрольні питання

1. Поясніть постановку завдання синтезу оптимального керування.

2. Запишіть вигляд функціоналів якості для систем 1), 2), 3), 4), (див. зміст роботи).

3. Сформулюйте принцип максимуму Понтрягіна.

4. Поясніть методику теоретичного синтезу оптимального керування в загальному вигляді і для двокритеріального завдання оптимального керування об’єктом з подвійним інтегруванням.

Лабораторна робота № 4

Ідентифікація статичних моделей об'єктів керування

Мета роботи: вивчення методики побудови статичних характеристик об'єктів керування методом найменших квадратів; дослідження властивостей МНК-оцінок.

Зміст роботи

Регресійний аналіз – це один з найпоширеніших методів побудови математичних залежностей на основі експериментальних даних з наступним виконанням статистичного аналізу результатів оцінювання параметрів.

Класичний регресійний аналіз ґрунтується на методі найменших квадратів (МНК) і його модифікаціях. МНК створений Лежандром і Гаусом на початку дев'ятнадцятого століття. Передумови застосування регресійного аналізу в завданнях побудови математичних моделей динамічних об'єктів (систем).

1. Прикладна теорія класичного регресійного аналізу, а також теорія регресійного аналізу з врахуванням порушення його канонічних передумов.

2. Зв'язок теорії планування експерименту з теорією регресійного аналізу.

3. Наявність великої кількості пакетів прикладних програм, що реалізують алгоритми регресійного аналізу.

4. Зручна форма представлення моделі об'єкта або у вигляді дискретної, або у вигляді безперервної передатної функції, що дозволяє без проміжних перетворень вирішувати завдання аналізу і синтезу цифрових алгоритмів керування.

5. Поширення алгоритмів регресійного аналізу на завдання оцінювання параметрів у реальному часі (рекурентно). На рисунку 15 наведена структура алгоритму регресійного аналізу.

Розглянемо лінійне рівняння регресії в загальному вигляді. Модель встановлює математичні співвідношення між показниками роботи об'єкта або характеристиками спостережуваного явища y ₁, y ₂,.., y_l та величинами, що їхобумовлюють –, x₁, x ₂,.., x _m. При цьому y – вихідні характеристики, відгуки, x – вхідні змінні, фактори.

Залежно від цілей дослідження математична модель може бути в різних термінах. Наприклад:

1. якщо необхідно досліджувати кінетику хімічних реакцій, то підходять аналітико-експериментальні моделі, складені на основі фізичних і хімічних закономірностях, а параметри визначаються експериментально;

2. якщо необхідно визначати оптимальний технологічний режим, то часто досить скористатися моделлю, що описує вихідні характеристики як поліноміальні функції факторів;

3. якщо за допомогою моделі необхідно розробити й настроїти САУ, то вона повинна відбивати зміна вхідних і вихідних характеристик у часі.

Рис. 15. Структура алгоритму регресійного аналізу

Існує велика кількість регресійних моделей:

– лінійні η = β ₁+ β ₂ x ₂+ β ₂ x ₂+...;

– нелінійні .

Під лінійною будемо розуміти модель лінійну по параметрах, наприклад η = β ₁+ β ₂ x ₁+ β ₃ x ₁∙ x ₂+ β ₄ x ₁∙ x ₃²+... не лінійна по факторам, але лінійна по коефіцієнтам регресії. Більшість модулів шляхом заміни можливо привести до лінійних.

Рівнянням регресії називається рівняння вигляду:

де y – виміряне значення вихідної змінної;

ε – шум;

η – дійсне значення відгуку;

x_j – вхідні сигнали, фактори;

f_i – довільні функції факторів експерименту (регресори);

β _i – коефіцієнти регресії.

Для статичних моделей: відгук – поліном по ступенях факторів. Подібна вистава опирається на той факт, що відгуки – часто безперервні функції від факторів і їх можна розкласти в ряд Тейлора в крапці x ₀=(x ₁⁰, x ₂⁰,.., x_m ⁰).

Необхідно відзначити, що важко описати поліномами функції неоднозначності, що мають розриви і (тобто де є стрибкоподібні зміни змінних), тому що вони в цих крапках не маю похідних (гістерезис, релейні характеристики).

Виходячи з вище наведеного лінійного рівняння регресії в класичному регресійному аналізі роблять наступні основні припущення.

1. Величина ε_l =1.. N, є випадкова величина. Тому, що η _l – не випадкова величина для детермінованого оператора, то y_l – теж випадкова величина.

2. Випадкова величина ε_l має нульове математичне очікування M { ε_l }=0. Якщо це не виконується, і M { ε_l }= v_l то заміняють η _l на η _l ′ а ε_l на ε_l ′ такі, що η _l ′=η _l+v _l, а ε_l′ = ε_l – M { ε_l }, тобто віднімають математичне очікування від випадкового сигналу і додають його до обмірюваних значень. Тому що ν постійна для будь-яких l, то вона діє на відгук однаково.

3. Значення випадкової величини ε_l не корелявоні і мають однакову дисперсію σ², тобто cov { ε_u, ε_l }= 0 при u ≠ l, а при u = l∙ σ²{ ε_l }=σ², тобто матриця cov { ε_u, ε_l } – діагональна. Тому що η _l – не випадкова величина, то σ²{ y_l }=σ², а cov { y_u, y_l }= 0 при u ≠ l, то є V (y) = I ·σ².

Припущення cov { ε_u, ε_l }=0 при u ≠ l часто не виконується для тимчасових рядів і інших випадків, коли спостереження статистично залежні для різних дослідів.

Припущення σ²{ ε_l }=σ² називається умовою однорідності або гомоскедастичності спостережень, якщо порушується, то спостереження неоднорідні, тобто інтенсивність випадкових збурень не змінюється при зміні факторів.

4.Випадкова величина ε_l має нормальний (Гаусовий) розподіл. Відповідно центральній граничній теоремі теорії ймовірностей вплив безлічі випадкових величин із приблизно однаковими дисперсіями еквівалентно впливу єдиної випадкової величини з нормальним законом розподілу.

Порушення цієї гіпотези тягне більш важкі наслідки.

5. Матриця регресорів:

де N – число спостережень;

k – число параметрів β.

Матриця F не випадкова. Припущення порушується, коли фактори x_j встановлюються або виміряються з помилками.

6. На значення параметрів β_i i =1,2,3,.., k не накладає ніяких обмежень, тобто попередньо про їхні значення нічого не відомо і при обчисленні вони можуть вийти якими завгодно.

7. Ранг матриці F дорівнює числу коефіцієнтів k, тобто rank (F)= k. rank – найвищий, відмінний від нуля, порядок мінору, тобто N ≥ k. Але іноді, коли між деякими стовпцями матриці F існує лінійна залежність.

Класичний регресійний аналіз – це процедура регресійних коефіцієнтів і статистичний аналіз моделі при виконанні всіх семи гіпотез. При порушенні кожного з пунктів процедура регресійного аналізу міняється.

Виведемо рівняння МНК.

де l =1.. N – кількість спостережень.

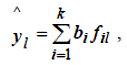
де y_l – прогнозоване значення відгуку і служить оцінкою дійсного значення y_l. Різниця e_l = yl – yl, називається залишками l = 1.. N.

Рівняння для оцінки можна в матричній формі:

де f – фактори.

Вимога – функції втрат (функція ризику) повинна прагнути до мінімуму.

Скалярний добуток вектора на самого себе рівно сумі квадратів його елементів.

Знайдемо мінімум:

Система лінійна щодо шуканих оцінок b₁, b₂,.., b_k,причому число рівнянь дорівнює числу невідомих. Const 2 не відіграє ролі, звідки випливає:

Покладемо:

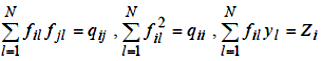
тоді: Gb = Z

де G – квадратна симетрична матриця, називана інформаційною матрицею.

Можна побачити, що: G = F^T · F, Z = F^T · y.

Тоді рівняння перепишеться:

Звідси можна записати основне рівняння МНК:

Розглянемо властивості МНК-оцінок.

При прийнятті розглянутих вище припущень (гіпотез) мають місце наступні властивості оцінок:

1. МНК-оцінки не зміщені.

де M {η} – не випадкова величина.

МНК не вносить в оцінки невідомих коефіцієнтів систематичної помилки. Якщо оцінки одержувати багаторазово для різних вибірок обсягу N, то вони будуть групуватися навколо математичного очікування M { b } = β.

2. Дисперсії і коваріації оцінок регресійних коефіцієнтів визначаються за формулою:

де C_ij – не діагональний елемент;

C_ii – діагональний елемент.

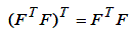– у силу симетричності.

2. Оцінки МНК ефективні, тобто мають найменші дисперсії серед усіх можливих лінійних незміщених оцінок.

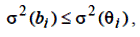
де θ _i – інші оцінки M {θ}= β, тобто

trV (b) ≤ trV (θ) – слід матриці коваріації.

де вище наведені вирази сума дисперсій.

Ця властивість означає, що точність МНК-оцінок в загальному випадку вище, чим точність інших незміщених оцінок. Визначник |V(b)| – узагальнена дисперсія. Таким чином МНК мінімізує узагальнену дисперсію.

4. МНК-оцінки самостійні, тобто коли число спостережень N прямує до нескінченності bin сходиться по ймовірності до β _i:

де ν – довільне мале позитивне число.

У математичній статистиці незміщені, ефективні заможні оцінки називають найкращими лінійними оцінками. Завдання ідентифікації статичної моделі об'єкта керування припускає визначення статичної характеристики за результатами обробки експериментальних даних. При наявності істотних зовнішніх збурень і перешкод ефективним методом рішення даного завдання є метод найменших квадратів (МНК) [6].

Розглянемо хімічний процес, що протікає в реакторі. Вхідними впливами є час реакції τ і температура реакції Т, вихідною величиною – процентний вміст корисного продукту хімічної реакції y. Відомий вид статичної характеристики:

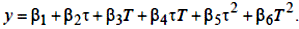
Необхідно визначити невідомі коефіцієнти β _i, i =1,6.

Для рішення поставленого завдання проведені експерименти. Значення вхідних впливів задавалися на одному із трьох рівнів кожний, вихід реакцій вимірявся для кожного експерименту. Результати експериментів представлені в табл. 5.

Таблиця 4.1

Результати проведених експериментів

№ експерименту	τ, год.	Т, ºС	y, %
1.
2.
3.
4.
5.	3,5	107,5
6.	3,5
7.		107,5
8.	3,5
9.		107,5

Відповідно до загальної процедури класичного МНК Введемо наступні позначення:

де x ₁ і x ₂ – фактори експерименту,

де f_i, i =1,6 – регресори,

де b_i - оцінка коефіцієнтів регресії β _i.

Сформуємо матрицю регресорів F і вектор вимірів y:

де f_ij – значення j -го фактора в i -му експерименті; y_i – значення виходу в i -му експерименті.

Тоді вектор МНК-оцінки коефіцієнтів регресії b = [ b ₁,.., b ₆] ^T визначається по формулі:

.

Можна показати, що при рівності рангу матриці F числу коефіцієнтів регресії, обчислені оцінки коефіцієнтів мінімізують суму квадратів помилки:

де N =9 – число експериментів; y_i – обмірюване значення виходу в i -му експерименті;

y_i – обчислене по отриманій моделі значення виходу в i -му експерименті.

Дата добавления: 2015-10-24