
Читайте также:
|
Пусть на отрезке  определена вещественнозначная функция
определена вещественнозначная функция  .
.
Рассмотрим разбиение отрезка 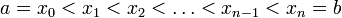 — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок
— конечное множество попарно различных точек отрезка. Это разбиение делит отрезок  на n отрезков
на n отрезков  . Длина наибольшего из отрезков
. Длина наибольшего из отрезков 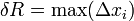 называется шагом разбиения, где
называется шагом разбиения, где 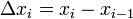 — длина элементарного отрезка.
— длина элементарного отрезка.
Отметим на каждом отрезке разбиения по точке  . Интегральной суммой называется выражение
. Интегральной суммой называется выражение  .
.
Если при стремлении шага разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора  , то это число называется интегралом функции
, то это число называется интегралом функции  на отрезке
на отрезке  , то есть
, то есть  .
.
Определенным интегралом от функции f(x) на отрезке [a,b] называют предел, к которому стремится интегральная сумма.
Теорема существования определённого интеграла. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема по этому отрезку.
Свойства:
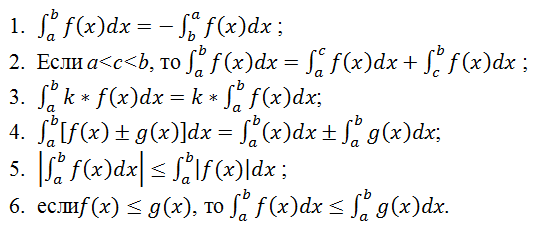
Правило. Для вычисления определенного интеграла от непрерывной функции надо найти для нее первообразную функцию и составить разность значений этой последней функции при верхнем и нижнем пределах интегрирования.

19. Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, длины дуги плоской кривой, объема тела.
 Пусть некоторая функция f(x) непрерывна на отрезке
Пусть некоторая функция f(x) непрерывна на отрезке  , и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой
, и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой  :
:
В предположение о непрерывности производной 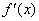 на [a,b], длина кривой AB выражается формулой:
на [a,b], длина кривой AB выражается формулой:
 или компактнее:
или компактнее: 
Рассмотрим случай параметрического задания кривой:
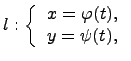
где t ∈ [a,b]. В этом случае для определения длина дуги  вычисляется определенный интеграл:
вычисляется определенный интеграл:

Рассмотрим случай, когда кривая задается в полярных координатах ρ=ρ(φ) где φ ∈ [α,β]. Тогда для определения длины дуги  вычисляется следующий определенный интеграл:
вычисляется следующий определенный интеграл:
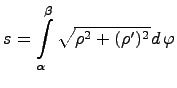
Вычисление объема тела вращения:
а) если тело образовано вращением криволинейной трапеции, ограниченной кривой y = f(x), осью OX и двумя прямыми x = a и x = b(a < b) вокруг оси OX, то объем тела  ;
;
б) а если тело образовано вращением фигуры, ограниченной кривой 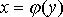 , прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем
, прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем  ;
;
в) если тело образовано вращением вокруг оси OY фигуры, ограниченной линией y = f (x), прямыми x = a, x = b (0≤a≤b) и осью OX, то его объем можно вычислить по формуле 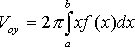 ;
;
г) если вращается вокруг полярной оси криволинейный сектор, ограниченный дугой  , двумя полярными радиусами
, двумя полярными радиусами 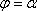 и
и  , то объем полученного тела может быть вычислен по формуле
, то объем полученного тела может быть вычислен по формуле  .
.
д)вычисление объема тела по площадям поперечных сечений
Пусть тело V расположено в пространстве между плоскостями x = a и x = b, и для 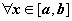 известна площадь его поперечного сечения S = S (x). Требуется определить объём этого тела.
известна площадь его поперечного сечения S = S (x). Требуется определить объём этого тела.
Рассечём это тело плоскостями x = x 0 = a, x = x 1, x = x 2, …, x = xi -1, x = xi, …, x = x n -1, x = xn = b на n слоёв (a = x 0< x 1 < < x 2< …< xn -1 < xn = b), на каждом из отрезков [ xi -1, xi ] возьмём произвольную точку  ; будем считать, что объём слоя, заключенного между плоскостями x = xi -1 и x = xi приближённо равен объёму
; будем считать, что объём слоя, заключенного между плоскостями x = xi -1 и x = xi приближённо равен объёму  цилиндрика с площадью основания
цилиндрика с площадью основания  и высотой
и высотой 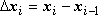 :
:  . Сумма объёмов
. Сумма объёмов  - объём ступенчатой фигуры - при
- объём ступенчатой фигуры - при  стремится к искомому объёму V, поэтому
стремится к искомому объёму V, поэтому  .
.
Дата добавления: 2015-08-20; просмотров: 264 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование гиперболических функций | | | Площадь поверхности вращения. |