
Читайте также:
|
Властивість 1. Крива K (див. означення) є самоподібною кривою із розмірністю самоподібності 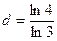 [13:62].
[13:62].
Доведення. Якщо взяти копію K, зменшену в три рази, то усю множину K можна скласти з чотирьох таких копій. Отже, крива K є самоподібною із розмірністю самоподібності 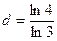 . Доведено.
. Доведено.
Властивість 2. Сніжинка Коха має нескінченну довжину.
Доведення. Досить показати, що кожний з трьох фракталів K, отриманих ітераціями (рис. 2.1), має нескінченну довжину. Нехай вихідний відрізок 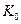 має одиничну довжину. Тоді довжина кривої
має одиничну довжину. Тоді довжина кривої 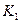 рівна
рівна  . Довжина кривої
. Довжина кривої 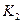 рівна
рівна 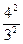 . Продовжуючи таким чином маємо, що крива
. Продовжуючи таким чином маємо, що крива 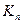 після n-го кроку має довжину
після n-го кроку має довжину 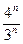 . Отже, довжина граничної кривої K рівна нескінченності:
. Отже, довжина граничної кривої K рівна нескінченності: 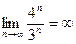 . А це і доводить, що сніжинка Коха має нескінченну довжину [8:19]. Доведено.
. А це і доводить, що сніжинка Коха має нескінченну довжину [8:19]. Доведено.
Властивість 3. Частина площини, яку обмежує сніжинка Коха, має площу  , де a – довжина сторони початкового рівностороннього трикутника.
, де a – довжина сторони початкового рівностороннього трикутника.
Доведення. Нехай 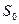 – площа початкового рівностороннього трикутника (нульовий крок), на першому кроці до нього добудовуємо три трикутники, площа кожного з яких рівна
– площа початкового рівностороннього трикутника (нульовий крок), на першому кроці до нього добудовуємо три трикутники, площа кожного з яких рівна  (бо сторона зменшилася в три рази). Отже, площа фігури, утвореної на першому кроці
(бо сторона зменшилася в три рази). Отже, площа фігури, утвореної на першому кроці  . На другому кроці додається ще
. На другому кроці додається ще 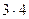 трикутники, площа кожного з яких дорівнює
трикутники, площа кожного з яких дорівнює 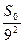 . Отже, площа фігури, одержаної на другому кроці буде
. Отже, площа фігури, одержаної на другому кроці буде 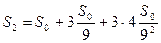 . На третьому кроці додаємо ще
. На третьому кроці додаємо ще 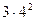 трикутники, площа кожного з яких дорівнює
трикутники, площа кожного з яких дорівнює 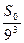 і загальна площа фігури після трьох кроків побудови буде
і загальна площа фігури після трьох кроків побудови буде 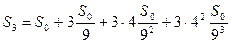 ,
, 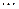 . На n-ому кроці до побудованої фігури добудуємо
. На n-ому кроці до побудованої фігури добудуємо  трикутники, площа кожного з яких
трикутники, площа кожного з яких 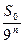 , загальна площа фігури після n кроків побудови буде
, загальна площа фігури після n кроків побудови буде 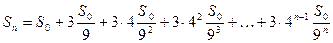 . Спрямувавши кількість кроків до нескінченності одержимо площу частини площини, обмеженої сніжинкою Коха.
. Спрямувавши кількість кроків до нескінченності одержимо площу частини площини, обмеженої сніжинкою Коха. 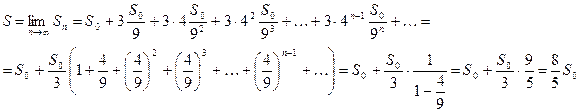
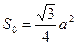 , де a - довжина сторони початкового рівностороннього трикутника. Отже,
, де a - довжина сторони початкового рівностороннього трикутника. Отже, 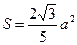 . Доведено.
. Доведено.
 Властивість 4. Точки
Властивість 4. Точки  і
і 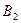 , що ділять відрізок
, що ділять відрізок  на три рівні частини, належать сніжинці Коха (рис. 2.4)[3].
на три рівні частини, належать сніжинці Коха (рис. 2.4)[3].
Доведення. Проведемо  ,
,  . Доведемо, що точки
. Доведемо, що точки  і
і 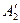 співпадають. Згідно означення сніжинки Коха
співпадають. Згідно означення сніжинки Коха 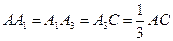 .
.
Трикутник 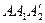 подібний трикутнику
подібний трикутнику 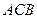 за двома кутами. Отже,
за двома кутами. Отже, 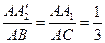 ,
, 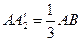 , таким чином,
, таким чином, 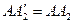 ,
, 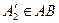 ,
, 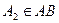 . Отже, точки
. Отже, точки  і
і 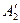 співпадають. Доведемо, що точка
співпадають. Доведемо, що точка  належить сніжинці Коха. Для цього покажемо, що
належить сніжинці Коха. Для цього покажемо, що  . З подібності трикутників
. З подібності трикутників 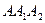 і
і 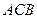 маємо
маємо 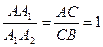 . Отже
. Отже 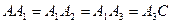 . Ми одержали, що трикутник
. Ми одержали, що трикутник 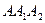 рівнобедрений із кутом
рівнобедрений із кутом 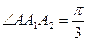 , бо
, бо 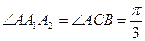 . Отже, трикутник
. Отже, трикутник 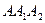 рівносторонній. Таким чином
рівносторонній. Таким чином  , а це і доводить, що точка
, а це і доводить, що точка  належить сніжинці Коха. Аналогічно доводиться, що точка
належить сніжинці Коха. Аналогічно доводиться, що точка 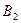 належить сніжинці Коха. Доведено.
належить сніжинці Коха. Доведено.
Наслідок. До сніжинки Коха можна приєднати шість сніжинок Коха, які подібні до початкової з коефіцієнтом подібності  , так, що кожна точка початкової сніжинки Коха належить принаймні одній з приєднаних сніжинок [3].
, так, що кожна точка початкової сніжинки Коха належить принаймні одній з приєднаних сніжинок [3].
Властивість 5. Крива К неперервна і не має дотичної в жодній своїй точці [28].
Дата добавления: 2015-08-21; просмотров: 246 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Cніжинка Коха | | | Острівець Коха та його властивості |