
Читайте также:
|
1. На числовой прямой отметить все нули подмодульных выражений (на каждом из полученных промежутков все подмодульные выражения сохраняют знак).
2. Раскрыть модули на каждом из найденных промежутков, предварительно определяя знак каждого подмодульного выражения на рассматриваемом промежутке (например, можно подставить в это выражение какое-либо значение аргумента из этого интервала).
3. Дальнейшие действия зависят от решаемой задачи.
Пример 1. Решить неравенство 
Решение. Так как 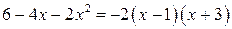 и
и  , то исходное неравенство эквивалентно неравенству
, то исходное неравенство эквивалентно неравенству 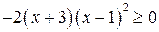 или
или 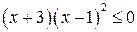 .
.
Исходное неравенство определено всюду и функция  равна нулю в точках
равна нулю в точках  .
.
На числовой оси отмечаем нули функции. (Отметим, что функция  существует для всех
существует для всех 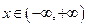 ).
).
Определим знаки  .
.
Определяем знак функции  , например, в точке
, например, в точке  . Имеем
. Имеем  .
.  Следовательно справа от точки
Следовательно справа от точки  функция
функция 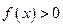 . При переходе через точку
. При переходе через точку  функция свой знак не меняет, так как корень
функция свой знак не меняет, так как корень  имеет четную кратность. Корень
имеет четную кратность. Корень  имеет нечетную кратность, поэтому при переходе через точку
имеет нечетную кратность, поэтому при переходе через точку  функция
функция  меняет свой знак.
меняет свой знак.

Ответ:  .
.
Пример 2. Используя метод интервалов, решить неравенство  .
.
Решение. Рассмотрим функцию  .
.
а) Так как  , то
, то 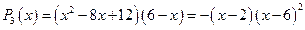 .
.
Так как  и
и  при любых действительных значениях
при любых действительных значениях  (дискриминант квадратного трехчлена отрицателен), то
(дискриминант квадратного трехчлена отрицателен), то  .
.
Исходное неравенство эквивалентно неравенству  или
или  .
.
б)  являются корнями знаменателя функции
являются корнями знаменателя функции  , поэтому эта функцияопределена для
, поэтому эта функцияопределена для  .
.
в)  являются корнями числителя функции
являются корнями числителя функции  . Это нули функции
. Это нули функции  .
.
На числовой оси отмечаем область определения и нули этой функции.
г) Определяем знаки функции  на интервалах знакопостоянства. (Можно, например, вычислить значения функции в точках
на интервалах знакопостоянства. (Можно, например, вычислить значения функции в точках  ,
,  ,
,  ,
,  и
и  .
.
В данном случае удобно исследовать знак функции  , пользуясь замечаниями 2 и 3.
, пользуясь замечаниями 2 и 3.
Определяем знак функции  , например, в точке
, например, в точке  имеем
имеем  .
.  Следовательно, справа от точки
Следовательно, справа от точки  функция
функция 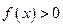 . При переходе через точку
. При переходе через точку  функция свой знак не меняет, так как корень
функция свой знак не меняет, так как корень  имеет четную кратность. Корни
имеет четную кратность. Корни 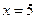 ,
,  ,
,  имеют нечетную кратность, поэтому на каждом из этих корней функция
имеют нечетную кратность, поэтому на каждом из этих корней функция  меняет свой знак.
меняет свой знак.

д) Записываем ответ.
Ответ:  .
.
Пример 3. Решить неравенство  .
.
Решение. Введем обозначение 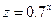 . Очевидно,
. Очевидно,  . Имеем
. Имеем 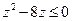 или
или 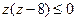 , откуда
, откуда 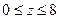 .
.  Учитывая, что
Учитывая, что  , имеем
, имеем  .
.
Решаем неравенство  .
.
Логарифмируем обе части последнего неравенства по основанию 0.7.
Учитывая, что функция  есть монотонно убывающая, имеем
есть монотонно убывающая, имеем  , откуда
, откуда 
Ответ:  .
.
Пример 4. Решить неравенство  .
.
Решение. Пусть  . Тогда исходное неравенство может быть записано в виде
. Тогда исходное неравенство может быть записано в виде  , откуда
, откуда 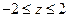 или
или  .
. 
Последнее неравенство может быть записано в виде  или
или  . Учитывая, что
. Учитывая, что  есть монотонно убывающая функция, имеем
есть монотонно убывающая функция, имеем  , откуда
, откуда  .
.
Ответ:  .
.
Пример 5. Решить неравенство:  .
.
Решение. Первый способ. Так как  то исходное неравенство равносильно совокупности двух систем неравенств:
то исходное неравенство равносильно совокупности двух систем неравенств:
а)  и б)
и б) 
Из системы а) имеем  или
или  .
.
Из системы б) имеем  или
или  .
.
Объединяя решения систем а) и б), имеем  .
.
Ответ: 
Второй способ.
а) Очевидно, что неравенство  справедливо при
справедливо при  , т. е. при
, т. е. при  .
.
 б) При
б) При  обе части исходного неравенства неотрицательны, поэтому
обе части исходного неравенства неотрицательны, поэтому  , откуда
, откуда 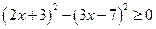 или
или  или
или  или
или 
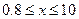 . Учитывая, что
. Учитывая, что  , имеем
, имеем  .
.
 Объединяя а) и б) получим
Объединяя а) и б) получим 
Ответ: 
Пример 6. Решить неравенство:  .
.
Решение. Так как  то исходное неравенство равносильно совокупности двух систем неравенств:
то исходное неравенство равносильно совокупности двух систем неравенств:
а)  и б)
и б) 
Из системы а) имеем  (система неравенств несовместна, т.е. не имеет решения).
(система неравенств несовместна, т.е. не имеет решения).
Из системы б) имеем  или
или  .
.
Объединяя решения систем а) и б), имеем  .
.
Ответ: 
Пример 7. Решить неравенство  .
.
Решение. Применим метод интервалов для выражений, содержащих модули.
На числовой оси отметим нули подмодульных выражений ( и
и  ).
).
На каждом из интервалов 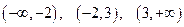 все подмодульные выражения сохраняют знак, поэтому исходное неравенство равносильно объединению трех систем:
все подмодульные выражения сохраняют знак, поэтому исходное неравенство равносильно объединению трех систем:
а)  б)
б) 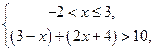 в)
в) 
Система а) эквивалентна системе  откуда
откуда 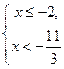 и
и 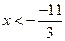 .
.
Система б) эквивалентна системе  откуда
откуда  Система б) несовместна.
Система б) несовместна.
Система в) эквивалентна системе  откуда
откуда  и
и  .
.
Объединяя а), б) и в), имеем  .
.
Ответ:  .
.
Пример 8. Решить уравнение  .
.
Решение. Данное уравнение равносильно совокупности двух уравнений  и
и  или
или 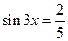 и
и 

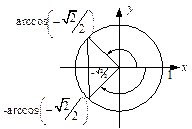
Из 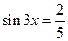 имеем
имеем  откуда
откуда 

 при
при  , откуда
, откуда 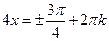 и
и  , где
, где 
Ответ: 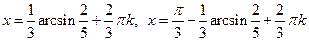 ,
,  (
( ).
).
Дата добавления: 2015-09-02; просмотров: 110 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Схема применения метода интервалов для дробно-рациональной функции | | | Эксплуатационного обслуживания |