Постановка вопроса
Задачи выпуклого программирования | Методом кусочно-линейной аппроксимации | выпуклого программирования градиентным методом. |
Модели выпуклого программирования
Постановка вопроса
Нелинейное программирование охватывает столь широкий класс задач, что универсальные эффективные численные методы решения для них в принципе не могут быть созданы. Это, в первую очередь, связано с тем, что в задачах нелинейного программирования, как правило, существуют такие допустимые (т.ею удовлетворяющие ограничениям) наборы параметров, которые являются наилучшими среди достаточно близких к ним допустимых наборов, но которые, тем не менее, не являются оптимальными, то есть, функция в этих точках не достигает глобального экстремума. Задачи такого типа называются многоэкстремальными или полимодальными.
Эффективные численные методы разработаны лишь для отдельных классов задач нелинейного программирования, про которые априори известно, что они не являются многоэкстремальными. Таковы, например, задачи выпуклого программирования.
Выпуклое программирование – это раздел нелинейного программирования, занимающийся исследованием и отысканием решений задачи минимизации выпуклой функции (максимизации вогнутой функции) на выпуклом множестве, заданном системой неравенств.











 Функция f(Х), определенная на выпуклом множестве М n-мерного пространства En, называется выпуклой на М, если для любых точек Х1 и Х2, принадлежащих М, и для любого числа λ, 0 ≤ λ≤1 справедливо неравенство
Функция f(Х), определенная на выпуклом множестве М n-мерного пространства En, называется выпуклой на М, если для любых точек Х1 и Х2, принадлежащих М, и для любого числа λ, 0 ≤ λ≤1 справедливо неравенство



 f((1- λ) Х1+ λ Х2) ≤(1- λ) f(Х1)+ λ f(Х2) (8.1)
f((1- λ) Х1+ λ Х2) ≤(1- λ) f(Х1)+ λ f(Х2) (8.1)
 т.е., график выпуклойфункции f(Х) расположен ниже (не выше) любой своей хорды (рис. 8.1).
т.е., график выпуклойфункции f(Х) расположен ниже (не выше) любой своей хорды (рис. 8.1).





 Иногда выпуклые функции называют выпуклыми вниз, а вогнутые – выпуклыми вверх.
Если в условии (8.1) знак ≤ изменить на ≥, получим определение вогнутой функции.
Иногда выпуклые функции называют выпуклыми вниз, а вогнутые – выпуклыми вверх.
Если в условии (8.1) знак ≤ изменить на ≥, получим определение вогнутой функции.
Если неравенство (8.1) выполняется как строгое, то функция называется строго выпуклой (или строго вогнутой).
Выпуклость (вогнутость) функции одной или двух переменных видна по ее графику.
В теории выпуклого программирования в качестве основной обычно рассматривается задача отыскания вектора  , который удовлетворяет условиям
, который удовлетворяет условиям
xj ≥ 0, j=1, 2, …, n (8.2)
gi(X) ≤ 0, i=1, 2, …, m (8.3)
и доставляет глобальный минимум функции F=f(x1, x2, …, xn). При этом заданные функции f, g1, g2, …, gm, определенные на n-мерных векторах X с неотрицательными компонентами, предполагаются выпуклыми.
Векторы, удовлетворяющие условиям (8.2) и (8.3), называются допустимыми, а искомые векторы 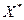 – оптимальными.
– оптимальными.
Дата добавления: 2015-09-01; просмотров: 71 | Нарушение авторских прав
mybiblioteka.su - 2015-2024 год. (0.012 сек.)












 Функция f(Х), определенная на выпуклом множестве М n-мерного пространства En, называется выпуклой на М, если для любых точек Х1 и Х2, принадлежащих М, и для любого числа λ, 0 ≤ λ≤1 справедливо неравенство
Функция f(Х), определенная на выпуклом множестве М n-мерного пространства En, называется выпуклой на М, если для любых точек Х1 и Х2, принадлежащих М, и для любого числа λ, 0 ≤ λ≤1 справедливо неравенство



 f((1- λ) Х1+ λ Х2) ≤(1- λ) f(Х1)+ λ f(Х2) (8.1)
f((1- λ) Х1+ λ Х2) ≤(1- λ) f(Х1)+ λ f(Х2) (8.1)
 т.е., график выпуклойфункции f(Х) расположен ниже (не выше) любой своей хорды (рис. 8.1).
т.е., график выпуклойфункции f(Х) расположен ниже (не выше) любой своей хорды (рис. 8.1).





 Иногда выпуклые функции называют выпуклыми вниз, а вогнутые – выпуклыми вверх.
Иногда выпуклые функции называют выпуклыми вниз, а вогнутые – выпуклыми вверх.
 , который удовлетворяет условиям
, который удовлетворяет условиям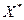 – оптимальными.
– оптимальными.