Методы минимизации 8

Метод парабол 5

Описание метода парабол 6

Основные шаги алгоритма метода парабол 8

Методы минимизации 8

Операции с выпуклыми функциями 17

Заключение 19

Литература 20

Введение

К задачам на поиск оптимума сводятся многие из проблем математики, экономики, техники, медицины и статистики. Среди различных методов решения задач нелинейного программирования важная роль отводится методам решения задачи безусловной оптимизации, которая состоит в нахождении минимума или максимума функции при отсутствии каких-либо ограничений. Изучение методов безусловной оптимизации необходимо по нескольким причинам. Во-первых, многие из задач оптимизации формулируются в виде задачи безусловной оптимизации. Во-вторых, значительное число алгоритмов решения задачи с ограничениями используют ее сведение к последовательности задач безусловной оптимизации.

Выпуклые функции и их свойства

Вводимые ниже классы функций и их свойства необходимы для анализа свойств сходимости релаксационных методов минимизации.

Функция f (x), 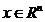, называется выпуклой, если

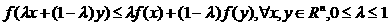. (1.1)

Функция f(x), 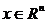, называется строго выпуклой, если в (1.1) при х¹y выполняется строгое неравенство.

Функция f (x), 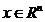, называется сильно выпуклой с константой 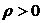, если при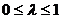

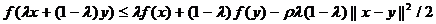. (1.2)

Для дифференцируемой функции f(x), 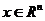, выпуклость эквивалентна неравенству

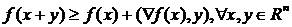, (1.3)

строгая выпуклость – неравенству

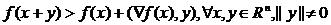, (1.4)

а сильная выпуклость – неравенству

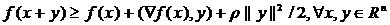. (1.5)

Из неравенств (2.3)–(2.5) вытекают следствия:

а) для выпуклой функции выполняется неравенство

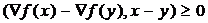; (1.6)

б) для строго выпуклой функции при x ¹ y выполняется строгое неравенство (2.6);

в) для сильно выпуклой функции выполняется неравенство

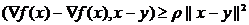. (1.7)

Для дважды дифференцируемой функции выпуклость эквивалентна условию 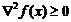, а сильная выпуклость – условию 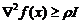для всех x.

Для дифференцируемой сильно выпуклой функции f(x) точка минимума x* (как мы увидим ниже) существует, единственна и 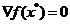. Поэтому из неравенств (2.5), (2.7) получим

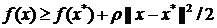, (1.8)

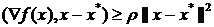, (1.9)

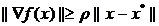. (1.10)

Для сильновыпуклой функции также справедлива оценка

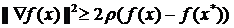. (1.11)

Оценка (2.11) дает верхнюю оценку возможного уменьшения функции в результате минимизации из точки x.

Для дифференцируемой функции, градиент которой удовлетворяет условию Липшица

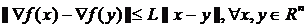, (1.12)

справедлива оценка

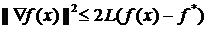, (1.13)

где f* удовлетворяет неравенству 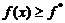для всех x.

Если функция выпукла и дифференцируема, а ее градиент удовлетворяет условию Липшица, тогда

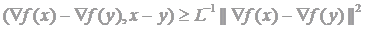
Дата добавления: 2015-09-01