Итеративные вычислительные методы.

Рассмотрим задачу НЛП

Где X допустимое множество (см. §1). Итеративными называются методы (или алгоритмические отображения), которые при помощи заданной начальной точки x₀ Î X генерируют последовательность допустимых точек x₀,x₁,…,x_k,x_k+1,…, последовательно приближающихся к оптимальному решению x* задачи (56). Переход от x_k к x_k+1 называется итерацией. Если за конечное число итераций метод (алгоритм) приводит к оптимальному решению, то он называется точным методом, в противном случае – приближенным методом. Обычно итерация строится по схеме

где вектор 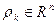называется направлением в точке x_k, а число - длинной шага. Различные итеративные методы отличаются друг от друга способом вычисления и .

Эффективность итеративного метода оценивается следующими факторами:

1) Универсальностью;

2) Надежностью и точностью;

3) Чувствительностью к исходным данным и параметрам;

4) Затратами на вычисление;

5) Сходимостью и скоростью сходимости;

Об этих факторах более подробно можно прочитать в [1], с. 252-254.

Говорят, что итеративный метод сходится, если генерируемая им последовательность {x_k} сходится к оптимальному решению.

Рассматривают сходимость по последовательности точек (x_k ® x*) или сходимость по целевой функции (f(x_k) ® f(x*)). В соответствии с этим могут быть заданы различные правила остановки итеративного процесса:

(57)

где e>0 называется точностью решения исходной задачи. При этом в качестве приближенного оптимального решения задачи (56) принимают . Важно отметить, что итеративные методы рассчитаны на применение ЭВМ. Желательным свойством итеративных процессов является свойство спуска:

f(x₀) ³ f(x₁) ³… ³ f(x_k) ³ f(x_k+1) ³…

Методы с таким свойством называются методами спуска. Различные методы 0-го, 1-го, 2-го и т.д. порядка, в зависимости от применения при вычислении направления и длины шага производных соответствующих порядков целевой функции. Методы 0-го порядка (когда производные не применяются), иногда называют методами поиска.

Итеративные методы для задач без ограничений (X = Rⁿ) упрощаются тем, что отсутствует необходимость проверки допустимости итеративных точек (x_k Î X) на каждой итерации. Методы, генерирующие только допустимые точки (их x_k Î X следует x_k+1 Î X), называют методами возможных направлений.

Наиболее простыми являются методы одномерной оптимизации, т.е. когда в (56) x Î R¹, а X = [a,b]. К таким методам относятся известные из курса анализа метода деления отрезка пополам, ломаных, касательных, парабол, покрытий. (см [2], с.9-69).

Непрерывную функцию f(x), x Î R¹, называют унимодальной на отрезке [a,b], если существуют точка x* Î [a,b], что на отрезке [a,x*] функция f(x) убывает, а на отрезке [x*,b] - возрастает. Основное свойство унимодальных функций, используемое при поиске точек минимума, состоит в том, что вычисление любых двух значений f(x₁), f(x₂), x₁ ¹ x₂, x₁,x₂ Î [a,b] позволяет уменьшить интервал поиска точки минимума. Для решения задачи одномерной оптимизации с унимодальной целевой функцией применяется метод золотого сечения и метод чисел Фибоначчи (см. [2] с. 19-22, [3] с. 194-204, [6] с. 109-114). В идейном отношении (и при реализации на ЭВМ) наиболее простым методом отыскания глобального минимума является метод равномерного перебора. Для сходимости этого метода важно, чтобы целевая функция удовлетворяла условию Липшица ([6] с. 114-116).

Известно, что градиент Ñf(x), как вектор, указывает направление возрастания функции f в точке x (любое достаточно малое перемещение из точки x в направлении вектора Ñf(x) увеличивает значение функции f). Это замечательное свойство положено в основу многих вычислительных методов. Итеративные методы, в которых направление r_x определяется при помощи градиента Ñf(x) (в задачах на максимум) и антиградиента -Ñf(x) (в задачах на минимум), называются градиентными методами (см. [1] с. 302-305, [2] с. 260-299, [6] с. 120-122). К числу градиентных можно отнести метод Ньютона, в котором r_k = -Ñf(x), a_k = [Ѳf(x_k)]^-1, а также методы наискорейшего спуска (см. там же), в которых длина шага определяется в результате решения оптимизационной задачи в направлении антиградиента.

Применение градиентных методов может оказаться неэффективным в задачах с «овражной» целевой функции, т.е. когда линии уровня целевой функции сильно вытянуты (имеют форму эллипсов) в окрестности оптимальной точки.

Если точка x_k лежит на границе допустимой области X, то любой малый шаг a_k >0 в направлении антиградиента может привести к недопустимой точке (x_k Ï X). Преодоление такого случая предусмотрено в методах возможных направлений (метод Зойтендейка, метод проекции градиента, метод условного градиента, выпуклый симплексный метод Зангвилла, [1] с. 371-466). Идея состоит в том, чтобы в граничной точке x_k выбрать направление поиска, соответствующее минимально возможному, с учетом ограничений, углу с направлением антиградиента в этой точке.

Пример 8. Методом проекции градиента решить следующую задачу НЛП:

при ограничениях

завершив вычисления при выполнении одного из условий:

На каждой итерации этого метода предусмотрена процедура возврата точки x_k+1 = x_k – a_kÑf(x_k) в допустимое множество X, если только x_k+1 Ï X. Такой возврат производится посредством проектирования Px_k+1 на X: x_k+1=P_x(x_k–a_kÑf(x_k)). При этом длину шага можно выбрать различными способами. Например, если Ñf(x) липшецева: ||Ñf(x’) – Ñf(x”)|| £ L||x ’- x”||, то полагают a_k = a Î (0;2/L).

Отметим, что вычисление проекции P_x(y), yÎRⁿ является самостоятельной задачей минимизации:

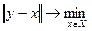
и может вызвать затруднения при сложных видах X. Однако, если X замкнутый шар , то известно, что

Решение: В качестве начальной точки возьмем x₀ = (0;0.5) Î X (здесь X={x Î R² | }). Так как

То полагаем a_k = a=0.75, k=0,1,…

Шаг 1.

Так как (0.75;-0.25) Î X, то x₁ = (0.75;-0.25).

Требуемая точность не достигнута, так как ||x₁ – x₀|| = 1.06 > 0.01.

Шаг 2.

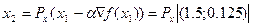
Поскольку точка (1.5;0.125) не принадлежит Х и учитывая то, что Х – замкнутый шар с радиусом r=1, получаем:

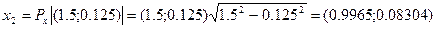
Требуемая точность не достигнута, так как ||x₂ – x₁|| = 0.298 > 0.01. И так далее. Требуемая точность получается на пятой итерации (шаге):

.

Таким образом, решение задачи найдено с точностью e=0.01. Заметим, что точное решение данной задачи есть x*=(1,0), f(x*)=-1.

Пример 9. Методом условного градиента решить следующую задачу НЛП:

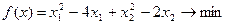
при ограничениях:

завершив вычисления при выполнении условия

Здесь f(x) выпуклая функция, а X = {x Î R² | } - прямоугольник (двумерный параллелепипед).

Пусть x_kÎX, причем Ñf(x_k)¹0. Тогда в малой окрестности точки x_k функция f(x) представима в виде:

и линейная функция f_k(x)=<Ñf(x_k),x-x_k>, является приближением разности f(x)-f(x_k) с точностью до малой величины O(||x-x_k||) в некоторой окрестности точки x_k (по определению градиента).

Поставим вспомогательную задачу:

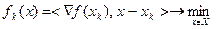(57)

Пусть - решение этой задачи. Положим

.

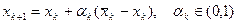В силу выпуклости множества Х, x_kÎX. Длину шага можно выбрать различными способами. Например, где 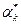найдено из условия наискорейшего спуска по направлению :

Отметим, что (57) является, вообще говоря, задачей НЛП и поэтому может оказаться достаточно сложной. Ее решение упрощается, если допустимое множество Х исходной задачи задано линейными ограничениями, либо имеет вид замкнутого шара или n-мерного параллелепипеда. В последнем случае, т.е. если , известно, что

(58)

где - i-я компонента вектора x_k.

Решение. В качестве начального приближения выберем точку x₀=(0,0)ÎX.

Шаг 1. Вычислим Ñf(x₀)=(-4,-2) и запишем задачу (57):

при ограничениях

Эту задачу ЛП можно решить симплекс-методом. В данном случае проще использовать формулу (58). Тогда . Найдем a₀. В данном случае

Из условия имеем . Поэтому a₀=min{1;0.8}=0.8.

Вычислим . Требуемая точность не достигнута, так как . Переходим ко второму шагу. И так далее.

Ответ: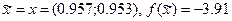

Векторы p₁,…,p_n называются сопряженными направлениями, если они линейно независимы и <Ѳf(x_k)p_i,p_j>=0 при i¹j. Заметим, что сопряженные направления определяются неоднозначно. Итерационные методы, использующие в качестве направлений последовательности сопряженных векторов, относятся к методам 2-го порядка и поэтому обладают большой точностью. В частности, если целевая функция квадратичная, то при помощи методов сопряженных направлений можно получить точку минимума за конечное число шагов. К таким методам относятся метод Дэвидона-Флетчера-Пауэлла, метод Флетчера и Ривса и метод Зангвилла ([1], с. 310-329).

Пример 10. Методом сопряженных направлений решить следующую задачу НЛП без ограничений:

Вычислим матрицу Гессе:

Построим два сопряженных направления p₁ и p₂. Положим p₁=(1,0). Тогда должен удовлетворять равенству 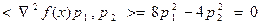. В частности, можно выбрать . Тогда и p₂=(1,2). Пусть минимизация начинается в точке x₀=(-1/2,1). Тогда вдоль p₁ получим точку x₁=(1/2,1). Теперь минимизируя f(x) из точки x₁ в направлении p₂ получим x₂=(1,2), которая является точкой глобального минимума.

Один из подходов к решению задачи НЛП (56) основан на замене этой задачи последовательностью задач безусловной минимизации:

(59)

где - функция, которая с ростом е во все большей степени учитывает ограничения, определяющие допустимое множество Х исходной задачи (56).

В методе штрафных функций подбираются так, чтобы при больших l функция f_l(x) из (59) мало отличалась от f(x) при xÎX, и быстро возрастала при удалении точки xÏX от допустимого множества X.

Последовательность функций { }, определенных в Rⁿ и обладающих свойствами

называется последовательностью штрафных функций множества Х.

Например, для задачи (1)-(3) положим:

(60)

где

,

Можно показать, что равенство (60) определяет последовательность штрафных функций допустимого множества Х, задаваемого соотношениями (2)-(3). Если последовательность решений задач (59)-(60) безусловной оптимизации сходится к пределу, то для достаточно больших l приближенное оптимальное решение задачи (1)-(3) полагают равным x_l. Критерием остановки служит неравенство ||x_l – x_l/2||£e, e>0,l - четное число.

Заметим, что для задачи (43)-(45) квадратичного программирования решения вспомогательной задачи (59) можно найти точно, применяя необходимые условия (а в случае выпуклости функции (43) и достаточные) вида (9).

Пример 11. Методом штрафных функций решить следующую задачу НЛП:

при ограничениях:

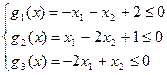
Так как целевая функция выпукла, а ограничения линейны, то решение x_l вспомогательной задачи (59) для любого l=1,2,… может быть найдено точно из условия Ñf_l(x_l)=0.

Решение. Предположим, что в точке x_l – решение задачи (59), g_i(x_l)>0 для всех i=1,2,3,…. Тогда . Поэтому (см. (60))

Решая систему уравнений

находим

Так как g₃(x_l)<0, то предположение не подтвердилось. Теперь предположим, что

Тогда

Поэтому считаем, что

Отсюда находим

(61)

Легко проверить, что второе предположение подтверждается, и равенство (61) определяет точку безусловного минимума x_l вспомогательной функции f_l(x) из (59). Окончательно находим:

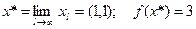
Отметим, что для решения вспомогательных задач (59) можно было использовать приближенные (напр. градиентные) методы. Тогда при требовании точности ||x_l – x_l/2||£e, e>0,l, получаем:

В методе барьерных функций исходная задача (56) также сводится к последовательности безусловных задач оптимизации (59), но функция Ф_k(x) выбирается так, чтобы при больших k функции f_k(x) из (59) мало отличались от f(x) при x Î int X, а при приближении к границе Х эти функции неограниченно возрастали. Последовательность функций {Ф_k(x)}, определенных в int X, называется последовательностью барьерных функций множества Х, если выполняются условия:

1)

2) 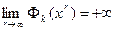для любой последовательности , сходящейся к граничной точке Х.

Например, для задачи (1)-(2) положим:

где

или .

Можно показать, что эти равенства определяют последовательность барьерных функций. Для достаточно больших k полагают x=x_k.

Пример 12. Методом барьерных функций решить следующую задачу НЛП с точностью e=0.002.

при ограничениях

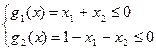
Задачу (59) запишем в виде:

Решая ее, например, методом Ньютона (применение этого метода см. на следующем примере) при k=500 и k=1000, получим: x₅₀₀=(0.6696;0.3319), x₁₀₀₀=(0.6682;0.3326). Так как ||x₁₀₀₀ - x₅₀₀||=1.65*10^-3<0.002, полагаем x= x₁₀₀₀, f(x)=0.6687.

Заканчивая обзор итеративных методов, еще раз отметим, что для решения задач безусловной оптимизации пригодны многие из упомянутых здесь методов, применяемых в условиях отсутствия ограничений: метод покоординатного спуска (при соблюдении условий спуска в качестве направлений выбираются координатные оси), метод градиентного наискорейшего спуска, метод Ньютона, метод сопряженных направлений и другие.

Пример 13. Методом Ньютона решить задачу НЛП безусловной оптимизации

с точностью e=0.05.

Итерационная формула этого метода есть

т.е. направление определяется антиградиентом, а длина шага – обратной матрицей Гессе. Будем пользоваться критерием остановки .

В качестве начальной точки возьмем x₀=(0.00;3.00). Вычислим поочередно

Отсюда находим

И так далее. Требуемая точность получается на 6-ом шаге. Поэтому

Для успешного и быстрого решения той или иной задачи важно уметь выбирать итеративный метод и начальное приближение (точку). Овладение такими навыками невозможно без достаточной практики по решению задач НЛП.

ЛИТЕРАТУРА

1. Базара М., Шетти К. Нелинейное программирование. Теория и алгоритмы. - М.,1982.
2. Васильев Ф.П. Численные методы решения экстремальных задач - М.,Наука,1988.
3. Габасов Р., Кирилова Ф.М. Методы оптимизации. - Минск, БГУ, 1981.
4. Карманов В.Г. Математическое программирование. - М., Наука, 1980.
5. Зангвилл У.Н. Нелинейное программирование. - М., Сов. радио, 1973.
6. Ногин В.Д. и др. Основы теории оптимизации. - М., Высш.шк., 1986.
7. Алексеев В.М. и др. Сборник задач по оптимизации. - М., Наука, 1984.

Дата добавления: 2015-09-04