II. Алгебраические дополнения

Алгебраическим дополнением А_ij элемента а_ij матрицы n -го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.

Пример 1. Найти алгебраические дополнения всех элементов матрицы

Решение:

7)Рассмотрим квадратную матрицу A n -го порядка.
Выберем i, j -ый элемент этой матрицы и вычеркнем i -ую строку и j -ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом M_{i j}:

.

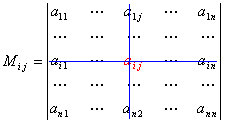Алгебраическое дополнение A_{i , j} элемента a_{i j} определяется формулой

.

Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:

.

8) Система линейных алгебраических уравнений с неизвестными — это система уравнений вида

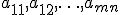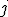Здесь — неизвестные, которые надо определить. Коэффициенты системы и её свободные члены предполагаются известными. Индексы коэффициента системы обозначают номера уравнения и неизвестного , при котором стоит этот коэффициент.

Система называется однородной, если все её свободные члены равны нулю, , иначе — неоднородной.

Система называется квадратной, если число уравнений равно числу неизвестных.

Решение системы уравнений — совокупность чисел , таких что подстановка каждого вместо в систему обращает все её уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.

Решения и 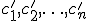совместной системы называются различными, если нарушается хотя бы одно из равенств:

Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма

Система линейных уравнений может быть представлена в матричной форме как

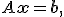
где

Пример системы линейных уравнений

Графическое решение системы линейных уравнений

Система из двух уравнений с двумя неизвестными имеет вид

Чтобы найти неизвестные нужно решить верхнее уравнение относительно : а затем подставить полученное решение в нижнее уравнение: Получено решение .

Данную систему можно наглядно изобразить на графике в виде двух прямых. Точка с координатами является ее решением.

Методы решения

Прямые (или точные) методы решения СЛАУ позволяют найти решение за определенное количество шагов. К прямым методам относятся метод Гаусса, метод Гаусса — Жордана, метод Крамера, матричный метод и метод прогонки (для трёхдиагональных матриц).

Итерационные методы основаны на использовании повторяющегося процесса. Они позволяют получить решение в результате последовательных приближений. К итерационным методам относятся метод Якоби (метод простой итерации), метод Гаусса — Зейделя,метод релаксации и многосеточный метод.

9) Решение системы линейных уравнений с использованием обратной матрицы.

Введем для системы линейных уравнений (1) следующие матрицы:
.
Систему (1) представим в матричной форме А * Х = В, которая эквивалентна исходной. Действительно, если перемножить матрицы А и Х и приравнять элементы матрицы-произведения к соответствующим элементам матрицы В, то получим систему уравнений (1).
Умножим обе части уравнения А * Х = В слева на матрицу А ^-1, получим А ^-1 * (А Х) = А ^-1 В или (А ^-1 А) Х = А ^-1 В.
Так как А ^-1 * А = Е, то Е*Х = А ^-1 * В или Х = А ^-1 * В.
Эта формула дает решение системы в матричной форме.
Пример. Решить систему
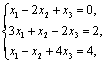используя обратную матрицу.
Решение. Найдем обратную матрицу к матрице системы .
Определитель матрицы А:
.
Так как определитель матрицы А отличен от 0, то обратная матрица существует. Найдем ее по формуле , вычислив предварительно алгебраические дополнения. Получим:
.
Найдем матричное решение системы:
.
Ответ: х ₁ = 1; х ₂ = 1; х ₃ = 1.

10) Правило Крамера

Пусть составленный из коэффициентов при неизвестных определитель:
.
Тогда система (1) имеет единственное решение
,
где определитель Δ _k (k=1,2,… n) получен из определителя Δ путем замены k -го столбца столбцом свободных членов системы (1).
Пример. Решить систему линейных уравнений по правилу Крамера:

Решение. Вычислим определители Δ, Δ₁, Δ₂, Δ_3.





Тогда .
Ответ: х ₁=1, х ₂=0, х ₃= -1.

11)

Декартовы прямоугольные системы координат

  Для задания декартовой прямоугольной системы координат нужно выбрать несколько взаимноперпендикулярных прямых, называемых осями. Точка пересечения осей O называется началом координат. На каждой оси нужно задать положительное направление и выбрать единицу масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P.

Рис. 2: Декартова плоскость  

Декартовыми прямоугольными координатами точки P на плоскости называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых - осей координат или, что то же, проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси.

Когда говорят про двухмерную систему коодинат, горизонтальную ось называют осьюабсцисс (осью Ox), вертикальную ось - осью ординат (осью Оy). Положительные направления выбирают на оси Ox - вправо, на оси Oy - вверх. Координаты x и y называются соответственно абсциссой и ординатой точки.

Запись P(a,b) означает, что точка P на плоскости имеет абсциссу a и ординату b.

Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до трех взаимно перпендикулярных координатных плоскостей или, что то же, проекции радиус-вектора r точки P на три взаимно перпендикулярные координатные оси.

В зависимости от взаимного расположения положительных направлений координатных осей возможны левая иправая координатные системы.

Рис. 3а: Левые координатные системы	Рис. 3б: Правые координатные системы

Как правило, пользуются правой координатной системой. Положительные направления выбирают: на оси Ox - на наблюдателя; на оси Oy - вправо; на оси Oz - вверх. Координаты x, y, z называются соответственно абсциссой, ординатой и аппликатой.

Координатными поверхностями, для которых одна из координат остается постоянной, здесь являются плоскости, параллельные координатным плоскостям, а координатными линиями, вдоль которых меняется только одна координата, - прямые, параллельные координатным осям. Координатные поверхности пересекаются по координатным линиям.

Запись P(a,b,c) означает, что точка Q имеет абсциссу a, ординату b и аппликату c.

12)

Полярные системы координат
	Рис. 4: Полярные системы координат   Полярными координатами точки P называются радиус-вектор ρ - расстояние от точки P до заданной точки O (полюса) и полярный угол φ - угол между прямой OP и заданной прямой, проходящей через полюс (полярной осью). Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным при отсчете в обратную сторону. Координатные линии в полярных системах - окружности с центром в полюсе и лучи. Формулы для перехода от полярных координат к декартовым x=ρ*cos(φ), y=ρ*sin(φ) и обратно: ρ=sqrt(x^2)+y^2), φ=arctg(y/x)=arcsin(y/ρ)

13)

Сферические системы координат
	Рис. 6: Сферические системы координат   r - длина радиус-вектора, φ - долгота, θ - полярное расстояние. Положительные направления отсчета показаны на рисунке 6. Если давать сферическим координатам значения в следующих пределах: 0 ≤ r < ∞, -π < φ ≤ π, 0 ≤ θ ≤ π, то получаются однозначно все точки пространства. Координатные поверхности: сферы с центром в начале (r=const), полуплоскости, ограниченные осью z (φ=const), конусы (с вершиной в начале), для которых ось z является осью (θ=const). Координатные линии - линии пересечения этих поверхностей. Формулы перехода от сферических координат к декартовым x=r*sin(θ)*cos(φ), y=r*sin(θ)*sin(φ), z=r*cos(φ) иобратно r=sqrt(x^2+y^2+z^2), φ=arctg(y/x), φ=arctg(sqrt((x^2+y^2)/z))

14)

Цилиндрические системы координат
	Рис. 5: Цилиндрические системы координат   ρ и φ - полярные координаты проекции точки P на основную плоскость (обычно xOy), z - аппликата - расстояние от точки P до основной плоскости. Для цилиндрических координат координатными поверхностями являются плоскости, перпендикулярные к оси Oz (z=const), полуплоскости, ограниченные осью z (φ=const) и цилиндрические поверхности, осью которых является ось z (ρ=const). Координатные линии - линии пересечения этих поверхностей. Формулы для перехода от цилиндрических координат к декартовым x=ρ*cos(φ), y=ρ*sin(φ), z=z и обратно: ρ=sqrt(x^2+y^2), φ=arctg(y/x)=arcsin(y/ρ)

15)

16) Операция сложения двух векторов - правило треугольника.

Покажем как происходит сложение двух векторов.

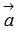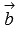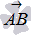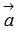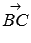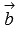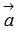Сложение векторов и происходит так: от произвольной точки A откладывается вектор , равный , далее от точки B откладываеься вектор , равный , и вектор представляет собой сумму векторов и 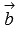. Такой способ сложения двух векторов назвается правилом треугольника.

Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.

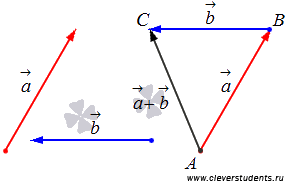
А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.

К началу страницы

Дата добавления: 2015-08-27