Читайте также:
|
Планы для квадратичных моделей.
Ортогональные центральные композиционные планы. Ротатабельные центральные композиционные планы.
Ортогональное композиционное планирование второго порядка. Для детального изучения области оптимума и участков поверхности отклика со значительной кривизной линейная модель становится неадекватной. В таких случаях для математического описания может быть достаточно полинома второго порядка, реже третьего порядка, полученного используя планы соответственно второго и третьего порядков.
Планы 2-го порядка позволяют получить математическое описание в виде полной квадратичной модели, содержащей кроме основных эффектов bi все парные взаимодействия bij и квадратичные эффекты bii.
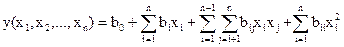
Подобные планы применяют, как правило, либо в том случае, когда использование планирования первого порядка не позволило получить адекватную регрессионную модель, и выяснилась необходимость ее усложнения, либо если заранее известно, что объект исследования обладает существенными нелинейными свойствами.
Планы 2k не могут обеспечить получение раздельных оценок коэффициентов bjj при квадратичных функциях и коэффициента b0.
Применение полного факторного эксперимента типа 3k для получения раздельных оценок коэффициентов полинома второго порядка не является рациональным, так как планирование на трех уровнях характеризуется резким увеличением объема эксперимента.
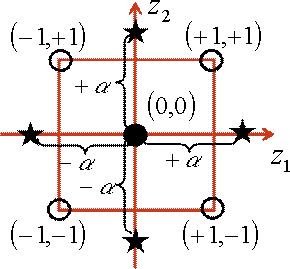
Целесообразнее для этой цели использовать композиционный план, образованный путем добавления некоторого количества специальных точек к «ядру», состоящему из планов 2k или 2k–p. Если к «ядру» добавить точку в центре плана с координатами (0, 0...0) и 2k так называемых «звездных» точек с координатами (±α, 0...0), (0, ±α,..0), …, (0, 0... ±α), то получим центральный композиционный план, предложенный Боксом. В качестве ядра используются точки ПФЭ – вершины квадрата и куба соответственно.
Используют эти планы обычно на заключительном этапе исследования: при описании экспериментальной области в ситуациях, когда отсутствует априорная информация об объекте и его полиномиальную модель приходится подбирать последовательно, начиная с простейшего линейного уравнения, которое затем достраивается до полной квадратичной модели. В таких случаях применение композиционных планов оказывается наиболее выгодным по числу опытов.
В зависимости от применяемого критерия оптимальности различают ортогональное и рототабельное композиционное планирование. Рассмотрим ортогональное композиционное планирование, в котором в силу ортогональности матрицы плана все коэффициенты квадратичной модели оцениваются независимо друг от друга.
Центрально–композиционные планы (ЦКП) любой модификации состоят из трех частей. Первая часть – основа или ядро плана – это ПФЭ 2k или ДФЭ 2k–p, где k – количество неизвестных коэффициентов регрессии, p = 0,1,2. При этом требуется, чтобы ядро плана обеспечивало раздельную оценку коэффициентов регрессии и всех парных взаимодействий. Данное условие накладывает весьма жесткое ограничение на возможную степень дробности используемого ДФЭ. В частности, при k £ 4, как показывают расчеты, может применяться лишь ПФЭ 2k; если 5 £ k £ 7, то кроме ПФЭ 2k можно использовать и ДФЭ 2k–1, а для k > 7 допустим также и ДФЭ 2k–2. Вторая часть ЦКП – так называемые «звездные» точки, расположенные на координатных осях на расстоянии ±α от центра эксперимента. Общее число таких точек равно 2k. Третья часть ЦКП – опыты в центре плана; число таких опытов N0 ³ 1. Произвольный симметричный ЦКП приведен в таблице:
| Составные части ЦКП | G | Факторы | Число точек | |||
| x1 | x2 | … | xk | |||
| Ядро плана (ПФЭ 2k или ДФЭ 2k–p) | –1 | –1 | … | –1 | 2k–p p=0;1;2; | |
| +1 | –1 | … | –1 | |||
| –1 | +1 | … | –1 | |||
| +1 | +1 | … | –1 | |||
| … | … | … | … | … | ||
| 2k–p | +1 | +1 | … | –1 | ||
| «Звездные» точки | 2k–p+1 | –a | … | 2k | ||
| 2k–p+2 | +a | … | ||||
| 2k–p+3 | –a | … | ||||
| 2k–p+4 | +a | … | ||||
| … | … | … | … | … | ||
| 2k–p+2k–1 | … | –a | ||||
| 2k–p+2k | … | +a | ||||
| Центральные точки | 2k–p+2k+1 | … | N0 | |||
| … | … | … | … | … | ||
| 2k–p+2k+N0 | … |
Общее число опытов N=2k+2k+1
Конкретные значения a и N0 выбираются исходя из тех или иных критериев оптимальности регрессионных экспериментов (a–звездное плечо, N0–количество экспериментов в центре плана). В связи с этим принято выделять ортогональные (ОЦКП) и рототабельные (РЦКП) центрально–композиционные планы.
В ОЦКП, как правило, N0 = 1, а план целиком строится с учетом критерия ортогональности (сумма по парных произведений значений уровней двух любых факторов (столбцов) равна нулю). Для обеспечения по парной ортогональности столбцов, отвечающих свободному члену b0 и квадратичным коэффициентам bi2, i = 1, 2, …, k, а также столбцов, отвечающих квадратичным членам между собой, необходимо принять специальные меры.
С этой целью, прежде всего, несколько видоизменяют систему базисных функций, а именно – ищут регрессионную модель в виде:
,
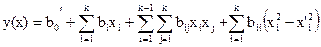где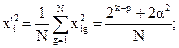 
N – общее число точек плана: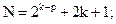 
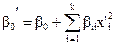(где p–число, определяющее дробность эксперимента, а 
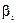– коэффициенты уравнения регрессии). Как видно, в этой модели при квадратичных коэффициентах используются центрированные переменные. Переход к таким переменным обеспечивает ортогональность столбца свободного члена уравнения регрессии (базисная функция f0 º 1), и любого из столбцов центрированных квадратов (базисная функция вида 
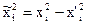). Действительно, для указанных столбцов имеет место следующее равенство:
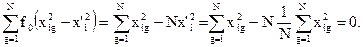
Это равенство справедливо независимо от конкретного значения a. Однако, при произвольном a, остаются неортогональными столбцы матрицы планирования, отвечающие различным центрированным квадратичным переменным. Поэтому, в ОЦКП числовое значение a и выбирается как раз из условия ортогональности именно этих столбцов, т.е. исходя из условия:
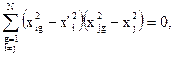
или, в развернутом виде:
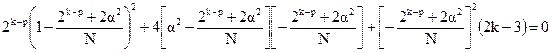
После несложных преобразований получаем уравнение для требуемого значения a:
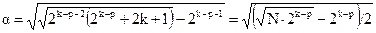
С помощью этой формулы найдены конкретные числовые значения a при n = 2 ¸ 8:
| N | ||||||||||||
| Ядро ЦПК | ПФЭ 22 | ПФЭ 23 | ПФЭ 24 | ПФЭ 25 | ДФЭ 25–1 | ПФЭ 26 | ДФЭ 26–1 | ПФЭ 27 | ДФЭ 27–1 | ПФЭ 28 | ДФЭ 28–1 | ДФЭ 28–2 |
| N | ||||||||||||
| a | 1,000 | 1,215 | 1,414 | 1,596 | 1,547 | 1,761 | 1,724 | 1,909 | 1,885 | 2,045 | 2,029 | 2,000 |
Общее количество опытов N в ОЦКП равно N = 2k–p+2k+ N0. Таким образом, переходя к квадратичной модели с центрированными квадратичными переменными и используя указанные значения a, можно добиться полной ортогонализации столбцов матрицы планирования.
| х0 | x1 | x2 | … | xk | x1x2 | … | xk–1xk | x12–x'12 | x22– x'22 | … | xk2– x'k2 |
| +1 | –1 | –1 | … | –1 | +1 | … | +1 | 1– x'12 | 1– x'22 | … | 1– x'k2 |
| +1 | +1 | –1 | … | –1 | –1 | … | +1 | 1– x'12 | 1– x'22 | … | 1– x'k2 |
| +1 | –1 | +1 | … | –1 | –1 | … | … | 1– x'12 | 1– x'22 | … | 1– x'k2 |
| +1 | +1 | +1 | … | –1 | +1 | … | … | 1– x'12 | 1– x'22 | … | 1– x'k2 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| +1 | +1 | +1 | … | +1 | +1 | … | +1 | 1– x'12 | 1– x'22 | … | 1– x'k2 |
| +1 | –a | … | … | a2– x'12 | – x'22 | … | – x'k2 | ||||
| +1 | +a | … | … | a2– x'12 | – x'22 | … | – x'k2 | ||||
| +1 | –a | … | … | – x'12 | a2– x'22 | … | – x'k2 | ||||
| +1 | +a | … | … | – x'12 | a2– x'22 | … | – x'k2 | ||||
| … | … | … | … | … | … | … | … | … | … | … | … |
| +1 | … | –a | … | – x'12 | – x'22 | … | a2– x'k2 | ||||
| +1 | … | +a | … | – x'12 | – x'22 | … | a2– x'k2 | ||||
| +1 | … | … | – x'12 | – x'22 | … | – x'k2 | |||||
| … | … | … | … | … | … | … | … | … | … | … | … |
| +1 | … | … | – x'12 | – x'22 | … | – x'k2 |
Следовательно, оценки коэффициентов регрессии, полученные с помощью ОЦКП, некоррелированы между собой, что, впрочем, характерно для любого ортогонального плана.
Реализация эксперимента по выбранной матрице планирования проводится также с дублированием опытов в каждой точке плана аналогично ПФЭ 2k.
Оценки коэффициентов регрессии для соответствующих групп равны:
Для свободного члена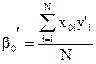 
;
Для линейных слагаемых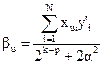 
, u = 1,2,…,k;
Для попарных взаимодействий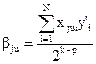 
, j, u = 1,2…k; j¹u;
Для центрированных квадратичных переменных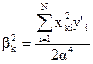 
.
Приведем теперь уравнение регрессии к более привычному для нас виду:
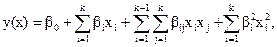
где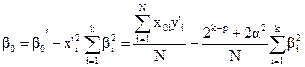 
Условие нормировки в случае ортогонального ЦКП не соблюдается, т.к.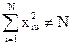 
(u – номер любого столбца, кроме нулевого). Это значит, что точность оценки коэффициентов регрессии для разных групп неодинакова.
Оценки дисперсий для каждой из четырех однородных групп для m параллельных опытов подсчитываются по следующим формулам:
;
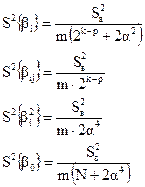где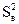 
– дисперсия воспроизводимости.
Таким образом, дисперсия оценки Y' функции отклика в некоторой точке факторного пространства зависит не только от расстояния этой точки до центра плана r, но и от ее положения на гиперсфере. Значит, ОЦКП не удовлетворяет условию рототабельности. Поэтому, если не предъявляются особые требования к точности предсказания выходной величины по уравнению регрессии в любом направлении факторного пространства от базовой точки, предпочтительно применение ортогонального ЦКП ввиду его простоты.
Рототабельный центральный композиционный план. При исследовании экстремальной области часто интерес представляет оценка не коэффициентов полученной регрессионной модели, а самой функции отклика. Кроме того, на практике часто можно значительно упростить регрессионную модель путем поворота координатных осей, т.е. преобразованием координат. Рототабельное планирование, обеспечивающее погрешность предсказания выходной величины по уравнению регрессии, зависящую лишь от расстояния точки факторного пространства до центра эксперимента, позволяет предсказывать с одинаковой точностью значение функции отклика, а, следовательно, преобразовывать систему координат с целью упрощения уравнения регрессии.
Основным условием рототабельности планов является инвариантность нормированной информационной матрицы Ф и корреляционной матрицы Ф–1 к вращению прямоугольных осей относительно начала координат, помещенного в базовую точку. Исходя из условия инвариантности матриц к вращению системы координат, точность оценок коэффициентов регрессии при вращении также не будет изменяться. Следует при этом отметить, что изменение момента масштаба входных переменных приводит к потере свойства рототабельности. Таким образом, необходимо поддерживать постоянство масштаба задания независимых переменных при проведении всего эксперимента.
Нормированная матрица Ф должна обладать некоторыми свойствами, чтобы быть инвариантной к ортогональному преобразованию (вращению).
Будем называть моментами плана элементы нормированной информационной матрицы:
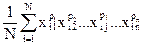
а порядком момента величину:
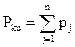
Момент будет четным, если все степени pj четные, и нечетные, если хотя бы одна степень pj элемента нормированной информационной матрицы нечетна.
Для рототабельного плана второго порядка все нечетные моменты вплоть до четвертого порядка включительно должны быть равны нулю. К таковым относятся следующие моменты:
Первого порядка
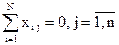
Второго порядка
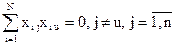
Третьего порядка
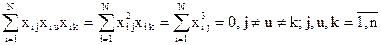
Четвертого порядка
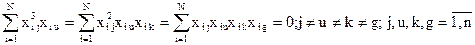
Нормированная информационная матрица Фишера рототабельного плана второго порядка имеет вид:
| x0 | x1 | x2 | … | xi | … | xn | X12 | x13 | … | xij | … | xn–1,n | x12 | x22 | … | xi2 | … | xn2 | ||||||||||
| x0 | … | … | … | … | L2 | L2 | … | L2 | … | L2 | ||||||||||||||||||
| x1 | L2 | … | … | ||0|| | ||0|| | |||||||||||||||||||||||
| x2 | L2 | … | … | |||||||||||||||||||||||||
| … | … | … | … | … | … | … | … | |||||||||||||||||||||
| xi | … | L2 | … | |||||||||||||||||||||||||
| … | … | … | … | … | … | … | … | |||||||||||||||||||||
| xn | … | … | L2 | |||||||||||||||||||||||||
| x12 | ||0|| | L4 | … | … | ||0|| | |||||||||||||||||||||||
| x13 | L4 | … | … | |||||||||||||||||||||||||
| … | … | … | … | … | … | … | … | |||||||||||||||||||||
| xii | … | L4 | … | |||||||||||||||||||||||||
| … | … | … | … | … | … | … | … | |||||||||||||||||||||
| xn–1,n | … | … | L4 | |||||||||||||||||||||||||
| x12 | L2 | ||0|| | ||0|| | 3L4 | L4 | … | L4 | … | L4 | |||||||||||||||||||
| x22 | L2 | L4 | 3L4 | … | L4 | … | L4 | |||||||||||||||||||||
| … | … | … | … | … | … | … | … | |||||||||||||||||||||
| xi2 | L2 | L4 | L4 | … | 3L4 | … | L4 | |||||||||||||||||||||
| … | … | … | … | … | … | … | … | |||||||||||||||||||||
| xn2 | L2 | L4 | L4 | … | L4 | … | 3L4 | |||||||||||||||||||||
Все четные моменты такого плана должны удовлетворять таким соотношениям:
Второго порядка
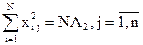
Четвертого порядка
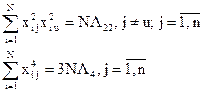
Решение задачи возможно в том случае, когда информационная матрица Фишера невырожденная. Определитель этой матрицы в качестве сомножителя содержит число ((n+2)L4–nL22). Поэтому условием невырожденности матрицы будет выполнение неравенства:
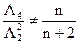
Константа L2 выбирается из условия выбора масштаба плана, а константа L4 выбирается из условия невырожденности информационной матрицы.
Если все точки плана расположить на поверхности сферы с радиусом r и с центром в начале координат нормированного факторного пространства, то дли любой I –ой точки данного плана можно записать:
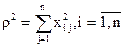
В соответствии с матрицей Фишера (подматрица с линейными членами):
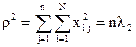
Можно выразить радиус сферы и через моменты четвертого порядка:
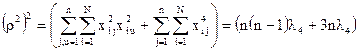
(выражение получено из подматриц с парными взаимодействиями и квадратичными членами).
Следовательно, из последних двух выражений: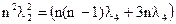 
Окончательно получим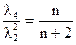 
т.е. условие невырожденности информационной матрицы Ф этого плана не выполняется.
Таким образом, точки рототабельного плана, в которых реализуются опыты, должны быть расположены на концентрических гиперсферах с общим центром.
Рототабельные планы – это планы, у которых точки плана располагаются на окружностях (сферах, гиперсферах). У рототабельного плана первого порядка точки плана располагаются на одной окружности (сфере, гиперсфере) с радиусом R
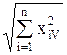=const=R,
где V =1,…, N – номер точки плана, i =1,…, n – номер фактора.
В таком случае точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая.
Рототабельный план может быть симметричным, когда точки плана располагаются симметрично друг друга. Рассмотренный ранее план ПФЭ 2n – рототабельный симметричный план первого порядка.
У рототабельных планов второго порядка точки плана располагаются на двух концентрических гиперсферах с радиусами R 1 и R 2. В таких планах
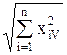=const1=R1,
,
для V =1,…, N0 и
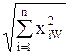=const2=R2,
для W=1,…, n0,
где V и W – текущие номера точек плана в двух подмножествах опытов N0 и n0 из их общего количества N, относящихся к двум разным концентрическим сферам. Одна из сфер может быть вырожденной, когда R 2=0. Рассмотренный ранее ортогональный центрально–композиционный план второго порядка (ОЦКП) не является рототабельным планом, так как его точки лежат на трех концентрических окружностях (сферах, гиперсферах).
Рототабельный план может быть ортогональным, если выполняется условие
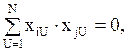
где i=1,…,m; j=1,…,m; m>n; i≠j – номера столбцов плана.
Рототабельный ортогональный центрально–композиционный план (РОЦКП) строится аналогично рассмотренному ранее ОЦКП. К использованному в качестве ядра плану ПФЭ 2n добавляются “звездные” точки – по две на каждый фактор и несколько точек в центре плана. “Звездные” точки должны располагаться на поверхности гиперсферы с радиусом R, на которой лежат и точки плана ПФЭ 2n, то есть величина плеча “звездных” точек 
должна равняться радиусу R. Это может быть обеспечено, при выполнении условия ортогональности, только при соответствующем выборе числа наблюдений в центральной (нулевой) точке плана n 0. Для РОЦКП n 0 зависит от числа факторов n. Напомним, что в ОЦКП n 0 = 1 для любого числа n.
Запишем общие выражения для всех четных моментов
1. Нулевого порядка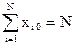 
2. Второго порядка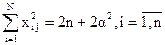 
3. Четвертого порядка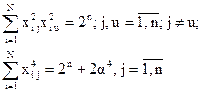 
Таким образом, NL2 = 2n+2a2, NL4 = 2n, 3NL4 = 2n+2a4.
Отсюда находим условие рототабельности: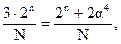 
или a4 = 2n.
Следовательно, чтобы ЦКП второго порядка обладал свойствами рототабельности, значение «звездного» плеча должно составлять: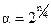 
Как и в случае ортогональных ЦКП, a зависит от числа n входных величин. Для определения числа опытов в центре плана («нулевой» точке) необходимо исходить из условия невырожденности информационной матрицы Фишера для рототабельных планов:
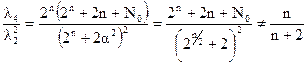
Из последнего соотношения видно, что для построения рототабельного ЦКП с невырожденной информационной матрицей Фишера достаточно в центре плана проводить один опыт. Увеличение числа N0 опытов в центре плана приводит к увеличению числителя и позволяет усилить неравенство до требуемой степени.
Часто исследователя интересует информация о функции отклика в некоторой окрестности центра плана, т.е. требуется, чтобы информация о выходной величине, полученная на основании уравнения регрессии, была практически одинаковой (постоянной) внутри гипершара радиуса r = 1 для r Î [0,1]. Такое планирование называется униформ–рототабельным. Для его получения достаточно обеспечить равенство дисперсии в центре плана (r = 0) и на поверхности гиперсферы радиуса r = 1. Этого добиваются подбором числа наблюдений N0 в центре плана.
В случае, когда число факторов велико, то в качестве «ядра» рототабельного ЦКП выбирается матрица ДФЭ. Оптимальное значение «звездного» плеча при этом определяется так: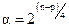 
В таблице приведены значения a и N0 для РЦКП, причем значения N0 приведены для униформ–рототабельного плана.
| n | |||||||||
| Ядро ЦПК | ПФЭ 22 | ПФЭ 23 | ПФЭ 24 | ПФЭ 25 | ДФЭ 25–1 | ПФЭ 26 | ДФЭ 26–1 | ПФЭ 27 | ДФЭ 27–1 |
| N0 | |||||||||
| N | |||||||||
| a | 1,414 | 1,682 | 2,000 | 2,378 | 2,000 | 2,828 | 2,378 | 3,364 | 2,828 |
Для нахождения методом наименьших квадратов оценки коэффициентов регрессии будем исходить из известного соотношения: СВ = FTY
откуда B = С–1FTY
Это равенство может быть переписано в виде B =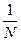 
Ф–1FTY
где Ф–1 – матрица, обратная нормированной информационной матрице Ф любого рототабельного плана.
Ввиду того, что подматрицы с линейными факторами, а также с их линейными взаимодействиями диагональные, то они легко обращаются (аналогично ортогональным планам).
Запишем формулы для определения оценок коэффициентов:
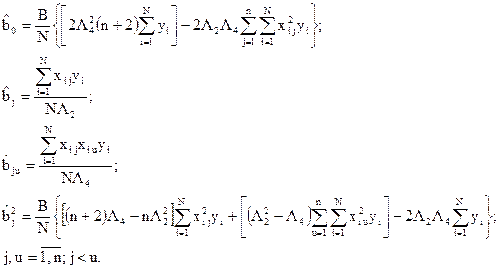
Точность вычисленных оценок определяется их дисперсиями. Для определения дисперсий оценок коэффициентов воспользуемся таблицей, в которой представлена матрица Ф–1,рассмотрев ее диагональные и недиагональные элементы. Поскольку в матрице недиагональные элементы не нулевые, то оценки коэффициентов регрессии квадратичных членов и оценка свободного члена остаются взаимозависимыми.
Исходя из системы оценок коэффициентов с учетом кратности m проведения опытов, получим:
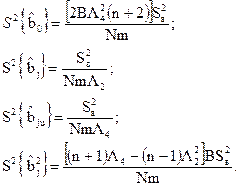
Вторые слагаемые в выражениях оценок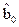 
и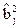 
обусловлены наличием корреляционной связи между ними. Найдем эту зависимость:
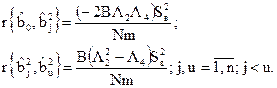
Поскольку остальные подматрицы нормированной матрицы Фишера Ф и обратной матрицы Ф–1 диагональные или нулевые, то все остальные корреляционные моменты равны нулю. Из этого следует, что оценки коэффициентов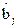 
и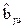 
при факторах и их линейных взаимодействиях независимы. Поэтому их можно проверять независимо от полученных оценок других групп коэффициентов на статистическую значимость на основании t–критерия Стьюдента, как и при ортогональном планировании. Если какой–либо из коэффициентов 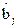или 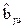окажется статистически незначимым, то его можно исключить из уравнения регрессии, не пересчитывая оценки других коэффициентов. Значимость оценки 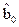свободного члена или оценки 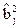квадратичных коэффициентов регрессии должна проверяться при фиксированных значениях всех остальных коэффициентов из этой группы с помощью F–критерия. Если какая–либо из оценок коэффициентов 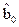или 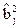окажется статистически незначимой, то для ее исключения из уравнения регрессии требуется пересчет остающихся оценок данной группы.
Рассмотрим задачу проверки гипотезы адекватности полученной регрессионной модели, содержащей значимые коэффициенты. Вначале будем предполагать, что параллельные опыты не ставятся, т.е. m = 1. Тогда остаточная сумма квадратов может быть записана:
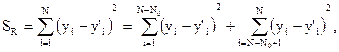
т.е. остаточная сумма разбита на сумму отклонений в точках ПФЭ (или ДФЭ), в «звездных» точках и на сумму отклонений опытных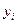 
и расчетных 
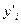значений выходной величины в центре плана. Y'i
Перепишем последнее выражение в виде:
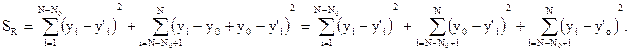В данном выражении первые два слагаемых связаны с общим рассеянием результатов наблюдений отклика относительно оценки регрессионной модели. Общее рассеяние связано со случайными погрешностями наблюдений, возникающими в результате влияния неконтролируемых факторов и систематическими погрешностями в случае неадекватности регрессионной модели и функции отклика. Третий член остаточной суммы связан с дисперсией, характеризующейся только случайной погрешностью опыта. Следовательно, с дисперсией адекватности (остаточной дисперсией) связана сумма:
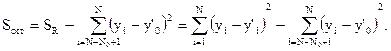
Подставим уравнение регрессии в это выражение:
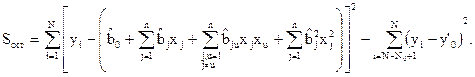
и получим остаточную сумму квадратов, связанную с дисперсией адекватности и имеющую число степеней свободы:
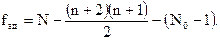
Если в каждой точке рототабельного центрального композиционного плана проводилось m параллельных опытов, то, проделав аналогичные выкладки, можно получить выражение для остаточной суммы, связанной с дисперсией адекватности. Оно будет отличаться заменой результатов 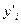единичных наблюдений в точках плана на средние арифметические 
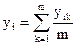единичных наблюдений, а среднего арифметического y0 из N0 параллельных наблюдений в центре плана на общее среднее арифметическое 
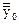из mN0 таких наблюдений, т.е.:
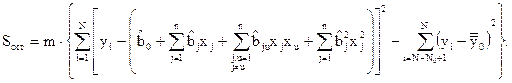
Данная остаточная сумма имеет то же число степеней свободы fад, что и предыдущая.
Далее для проверки адекватности модели необходимо для отношения дисперсии адекватности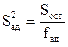 
и дисперсии воспроизводимости применить F–критерий Фишера, как и в общем случае регрессионного анализа. Полученная адекватная модель позволяет не только предсказать с равной точностью независимо от направления значение величины отклика, но и оценить ординаты точки экстремума. Ввиду свойства рототабельности плана эта задача облегчается – можно от полинома второго порядка, полученного в результате эксперимента, преобразованием системы координат (поворотом координатных осей) перейти к стандартному каноническому уравнению.
В таблице приведена матрица рототабельного n–мерного плана второго порядка, в которой используется обозначение:
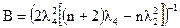
Нормированная обратная информационная матрица Фишера рототабельного плана второго порядка имеет вид:
| X0 | x1 | x2 | … | xn | x12 | x13 | … | xn–1,n | x12 | x22 | … | xn2 | |
| x0 | 2BL42(n+2) | … | … | –2BL2L4 | –2BL2L4 | … | –2BL2L4 | ||||||
| x1 | L2–1 | … | ||0|| | ||0|| | |||||||||
| x2 | L2–1 | … | |||||||||||
| … | … | … | … | … | … | ||||||||
| xn | … | L2–1 | |||||||||||
| x12 | ||0|| | L4–1 | … | ||0|| | |||||||||
| x13 | L4–1 | … | |||||||||||
| … | … | … | … | … | … | ||||||||
| xn–1,n | … | L4–1 | |||||||||||
| x12 | –2BL2L4 | ||0|| | ||0|| | B[(n+1)L4––(n–1)L22] | B(L22–L4) | … | B(L22–L4) | ||||||
| x22 | –2BL2L4 | B(L22–L4) | B[(n+1)L4– –(n–1)L22] | … | B(L22–L4) | ||||||||
| … | … | … | … | … | … | ||||||||
| xn2 | –2BL2L4 | B(L22–L4) | B(L22–L4) | … | B[(n+1)L4– –(n–1)L22] |
Параметры РОЦКП в зависимости от числа факторов
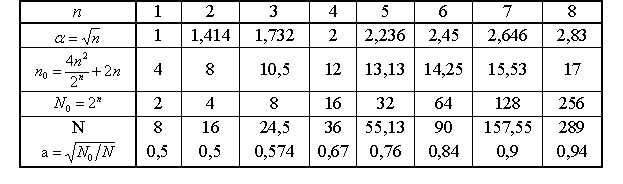
В [1] без вывода для РОЦКП рекомендуется принимать
.
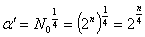Тогда
.
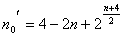Параметры РОЦКП по [1]
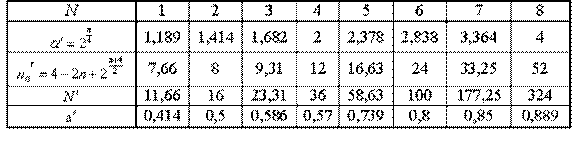
Пример рототабельного ортогонального центрально-композиционного плана для n = 2.
Параметры плана:
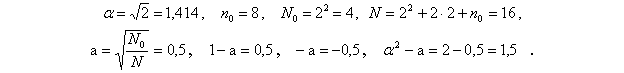
Нет необходимости проводить восемь раз (точки с 9 по 16) опыты в центре плана. Достаточно провести этот опыт один раз и записать результат во все восемь строк. Строки сокращать нельзя, так как нарушается свойство ортогональности, и коэффициенты полинома будут определены неверно.
Коэффициенты квадратичного полинома рассчитаются, как и ранее.
Использован рассмотренный ранее план ПФЭ 22 с добавленными опытами 5-16.
,
, 
,
,
,
.
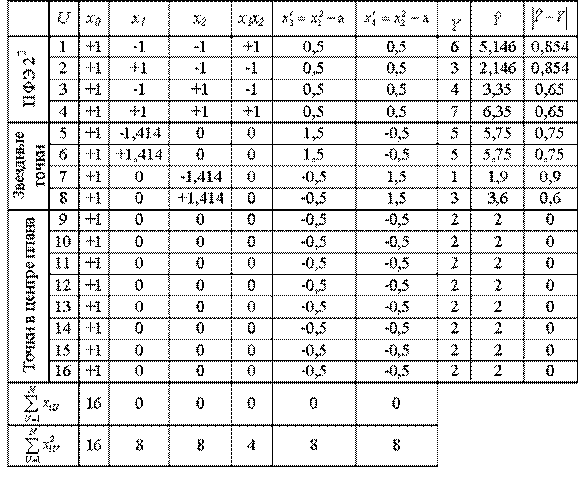
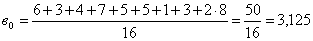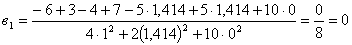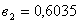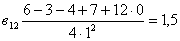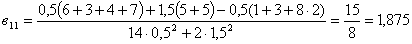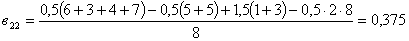Полином принимает вид
.
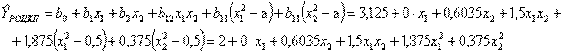Рассчитанные значения функции и расхождения с опытными данными представлены в предпоследнем и последнем столбцах плана.
Ранее для ОЦКП, при несколько отличающейся поверхности функции, был получен близкий полином в виде
.
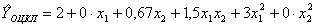Для n=2 число членов квадратичного полинома составляет шесть. В ОЦКП и РОЦКП необходимо провести девять отличающихся опытов при пяти уровнях варьирования факторов. Поэтому ОЦКП и РОЦКП - ненасыщенные планы. Такое число экспериментальных точек может быть использовано для построения, например, кубичных полиномов.
СПИСОК ЛИТЕРАТУРЫ
1. Максимова О.В. Теория вероятностей и математическая статистика: Учеб. пособие – М.: Издательско-торговая корпорация «Дашков и Ко», 2006. – 320 с.
2. Брандт З. Анализ данных. Статистические и вычислительные методы для научных работников и инженеров: Пер. с англ. – М.: Мир, ООО «Издательство АСТ», 2003. – 686 с.
3. Павлов С.В. Теория вероятностей и математическая статистика: Учеб. пособие – М.: РИОР, 2006. – 186 с.
4. Адлер Ю.П. Введение в планирование эксперимента / Ю.П. Адлер. – М.: Металлургия, 1969. – 157 с.
5. Румшиский Л.З. Математическая обработка результатов эксперимента: Справ. руководство / Л.З. Румшиский. – М.: Наука, 1971. – 192 с.
6. Назаров Н.Г. Измерения: планирование и обработка результатов / Н.Г. Назаров. – М.: Изд-во стандартов, 2000. – 302 с.
7. Планирование эксперимента в исследовании технологических процессов / К. Хартман [и др.] / Под ред. Э.К. Лецкого. – М.: Мир, 1977. – 552 с.
8. Кадомская К.П. Методы обработки экспериментальных результатов и планирование эксперимента: Учебное пособие.-Новосибирск: изд-во НГТУ-2002.-72 с.
9. Львовский Е.Н. Статистические методы построения эмпирических формул. Учебное пособие для вузов. -М.:Высшая школа.-1988.-239 с.
10. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Методы обработки данных. М.:Мир.-1980.-510 с.
Дата добавления: 2015-08-20; просмотров: 170 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лекция 13. | | | Вступление 1 страница |