в сезонном анализе

Использование фиктивных переменных

в сезонном анализе

в ситуациях, когда в ходе сбора исходных статистических данных имеет место косвенное воздействие (во времени и/или в пространстве) некоторых качественных факторов, в результате которого происходят скачкообразные сдвиги в структуре анализируемых линейных связей (т.е. в значениях коэффициентов регрессии), для оценивания параметров функций регрессий привлекают подходы, связанные с введением в правую часть регрессионного уравнения определенного числа фиктивных (дихотомических, бинарных, булевых) переменных. Такие переменные могут принимать одно из двух возможных значений (ноль или единица), и тем самым отражают два противоположных состояния качественного фак­тора: фактор действует – фактор не действует (курс валюты фиксированный – курс валюты плавающий; сезон летний – сезон зимний и т.д.).

Построение модели осуществляется с помощью аддитивного добавления в правую часть регрессионного уравнения бинарных переменных, которые могут принимать лишь два значения: нуль или единица.

Пусть переменная Y определяется количественной переменной Х, причем эта зависимость существенно разнится по кварталам. (В качестве переменной Х может выступать переменная t, означающая влияние фактора времени). Тогда общую модель такой ситуации можно представить в виде:

Y_t = β₀ + β₁X_t + α₁Z₁ + α₂Z₂ + α₃Z₃ + ε_t, (4.8)

где Z_j – фиктивные переменные, введенные для описания сезонных различий:

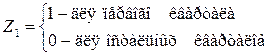
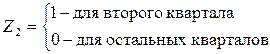
Следует отметить, что число фиктивных переменных Z_j должно быть на единицу меньше, чем число кварталов (в противном случае будет иметь место линейная зависимость между переменными Z_j, т.е. мультиколлинеарность).

В рассматриваемом случае четвертый квартал выступает в качестве базы для сравнения сезонных изменений (для него не ввели фиктивную переменную).

Если значения Y_t существенно различаются по кварталам (сезонам), то в уравнении (4.8) коэффициенты при фиктивных переменных окажутся статистически значимыми. Тогда ожидаемое значение Y по кварталам определится следующими соотношениями:

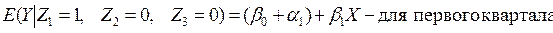
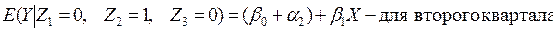
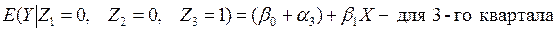
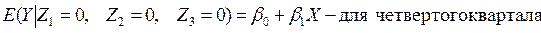
Видим, что в модели (4.8) рассматриваются такие ситуации, при которых квартальные различия отражаются лишь в различии свободных членов моделей.

Можно усреднить четыре полученные линии регрессии. Тогда расстояния между отдельной регрессионной прямой для любого квартала и усредненной моделью даст оценку сезонных отклонений в этом квартале. Очевидно, что для аддитивной модели сумма сезонных отклонений будет равна нулю.

Если же различия затрагивают и изменение коэффициента регрессии при объясняющей переменной Х, то это может быть учтено в следующей модели:

Y_t = β₀ + β₁X_t + α₁Z₁ + α₂Z₂ + α₃Z₃ +

+ α₄Z₁ X_t + α₅Z₂ X_t + α₆Z₃ X_t + ε_t, (4.9)

где коэффициенты a₄, a₅, a₆, связанные с произведениями Х и Z, называются дифференциальными угловыми коэффициентами.

Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, так как вполне вероятны ошибки спецификации. Поэтому рекомендуется следующая схема выбора модели.

Вначале строится модель (4.9) и оценивается статистическая значимость коэффициентов. Если дифференциальные угловые коэффициенты оказываются незначимыми, то переходят к модели (4.8). Если в этой модели дифференциальные свободные члены оказываются статистически незначимыми, то делают вывод, что квартальные (сезонные) изменения несущественны для рассматриваемой зависимости.

Пример 10. В табл. 4.17 представлены расходы потребителей на газ и электричество в США в постоянных ценах с 1 квартала 1997 г. по 4 квартал 2002 г.

Таблица 4.17 – расходы потребителей на газ и электричество

Год	Квартал	Y	t	Z2	Z3	Z4
		7,33
	4,7
	5,1
	5,46
		7,65
	4,92
	5,15
	5,55
		7,96
	5,01
	5,05
	5,59
		7,74
	5,1
	5,67
	5,92
		8,04
	5,27
	5,51
	6,04
		8,26
	5,51
	5,41
	5,83

На рис. 4.7 представлено графическое изображение рассматриваемого временного ряда.

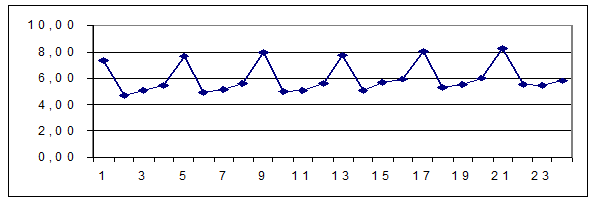Рис. 4.7. график изменения расходов потребителей на газ и электричество

Ряд характеризуется небольшой тенденцией к повышению и сильными сезонными колебаниями. Как и следовало предполагать, расходы такого рода всегда значительнее зимой, чем летом.

Возьмем, например, первый квартал в качестве базового (эталонного) и будем использовать фиктивные переменные для оценки различий между ним и другими кварталами. Запишем модель следующим образом:

У = b₀ + b₁t + a₂Z₂ + a₃Z₃ + a₄Z₄ + e

где

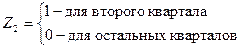
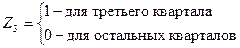
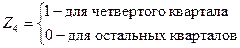
Коэффициенты a₂, a₃, a₄ дают численную оценку эффекта, вызываемого сменой сезонов. Коэффициент a₂ показывает дополнительное потребление газа и электроэнергии во 2-м квартале по сравнению с первым кварталом, связанное с изменением времени года. Аналогично, a₃ и a₄ показывают соответствующие дополнительные количества в 3 и 4 кварталах относительно 1-го квартала (базового).

Оценив регрессионную зависимость расходов от времени и фиктивных переменных методом наименьших квадратов (с помощью функции ЛИНЕЙН), получаем:

	-2,1931	-2,57818	-2,77659	0,031589	7,482518
	0,084642	0,084087	0,083752	0,004329	0,075929
	0,986654	0,144869	#Н/Д	#Н/Д	#Н/Д
	351,1631		#Н/Д	#Н/Д	#Н/Д
	29,47954	0,398754	#Н/Д	#Н/Д	#Н/Д
t	-25,9102	-30,6608	-33,1524	7,297479	98,54636

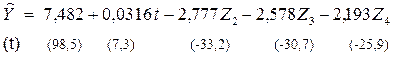(4.10)

R² = 0,987, F = 351.

Все t-тесты, относящиеся к коэффициентам при фиктивных переменных показывают высокую значимость, как и F-тест для их совместной объясняющей способности.

Из этого результата выводим отдельные уравнения, характеризующие динамику уровней ряда, для каждого квартала:

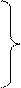
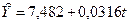- 1-й квартал,

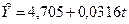- 2-й квартал, (7,482 – 2,777= 4,705)

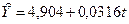- 3-й квартал, (4.11) (7,482 – 2,578 = 4,904)

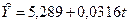- 4-й квартал. (7,482 – 2,193 = 5,289)

Результаты моделирования представлены на рис…

При необходимости можно использовать оцененную регрессию для получения оценки сезонных колебаний в каждом квартале. Выражение (4.11) дает 4 отдельные линии регрессии. Усредняя их, получаем:

,

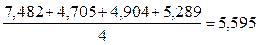или .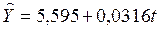

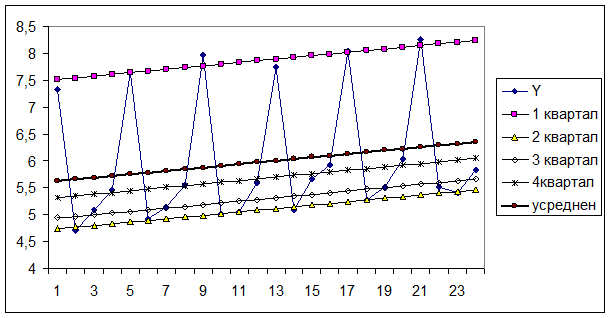
Рис. 4.8

Расстояние между отдельной линией регрессии для любого квартала и усредненной линией (см. рис. 4.8), представленное разностью значений свободного члена в уравнении регрессии, дает оценку сезонных отклонений в этом квартале, которая составила:

для 1 квартала 7,482 – 5,595 = 1,887,

для 2 квартала 4,705 – 5,595 = -0,89,

для 3 квартала 4,904 – 5,595 = -0,691,

для 4 квартала 5,289 – 5,595 = -0,306.

(Проверка: сумма сезонных отклонений должна равняться нулю, и в данном случае это правило выполняется).

Пример 11. В таблице 4.18 представлены данные, характеризующие объем продаж некоторого продукта (см. пример 8) в течение последних 13 кварталов (Y_t), дополненные ценой этого продукта (Х_t).

Таблица 4.18 – объем продаж и цена некоторого продукта

Период	t	Yt	Xt	Z1	Z2	Z3
2002г., 1 кв.
2 кв.
3 кв.			12,5
4 кв.
2003г., 1 кв.
2 кв.
3 кв.
4 кв.			17,3
2004г., 1 кв.
2 кв.			19,5
3 кв.
4 кв.
2005г., 1 кв.			25,5

На рис. 4.9 и 4.10 показана динамика объема продаж и цен соответственно.

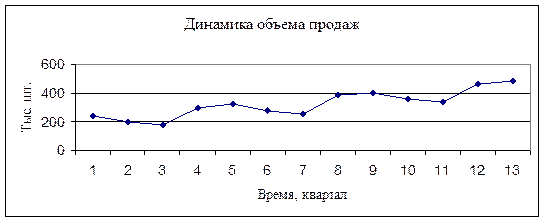
Рис. 4.9

Из рис. 4.9 видим, что объем продаж с течением времени растет и при этом имеет ярко выраженные сезонные изменения: в первом и четвертом кварталах продажи значительно выше, чем во втором и четвертом.

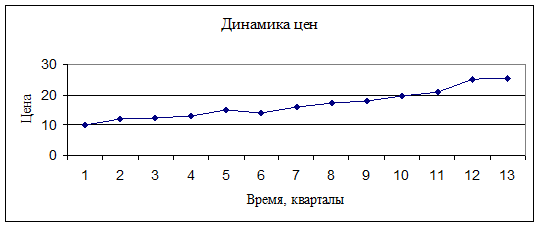
Рис. 4.10

Цена имеет тенденцию роста (рис. 4.10), сезонных изменений при этом не наблюдается.

Для построения модели зависимости объема продаж от цены с учетом сезонного характера спроса на этот продукт воспользуемся фиктивными переменными:

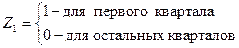
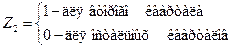
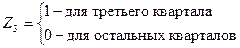
Четвертый квартал рассматриваем как базовый. Фиктивные переменные – в табл. 4.18 (столбцы 5 – 7). Модель строим в виде (4.9):

Y_t = β₀ + β₁X_t + α₁Z₁ + α₂Z₂ + α₃Z₃ +

+ α₄Z₁ X_t + α₅Z₂ X_t + α₆Z₃ X_t + ε_t,

Применив метод наименьших квадратов, получили оценки параметров модели (табл. 4.19):

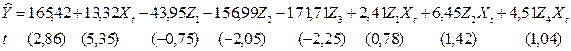
R² = 0,978; F = 32,01 > F_{0,05; 5; 8} = 4,82.

Таблица 4.19

α6	α5	α4	α3	α2	α1	β1	β0
4,512954341	6,539216355	2,430681	-171,707	-156,991	-43,9449	13,32266	135,4189
4,320538718	4,61418654	3,128082	76,17686	76,67322	58,50386	2,483976	47,41922
0,978171412	21,35737703	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д
32,00820322		#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д
102201,0045	2280,687767	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д
t =1,044535	t =1,417198	t =0,777	t =-2,254	t =-2,048	t =-0,751	t =5,363	t =2,855

Величина t-статистик свидетельствует о том, что при уровне значимости 10% статистически значимыми можно считать оценки параметров β₀, β₁, α₂, α₃ (критическое значение t _{0,1; 5} = 2,01).

Поскольку дифференциальные угловые коэффициенты оказались незначимыми, то перейдем к модели (4.8):

Y_t = β₀ + β₁X_t + α₁Z₁ + α₂Z₂ + α₃Z₃ + ε_t.

Результаты оценивания параметров этой модели представлены в табл. 4.20.

Таблица 4.20

α3	α2	α1	β1	β0
-92,3968	-49,6244	0,959941	15,82925	89,21408
16,96689	17,28776	15,79303	1,259083	26,06985
0,967617	20,56514	#Н/Д	#Н/Д	#Н/Д
59,76138		#Н/Д	#Н/Д	#Н/Д
101098,3	3383,399	#Н/Д	#Н/Д	#Н/Д
t =-5,446	t =-2,87	t =0,0608	t =12,572	t =3,4221

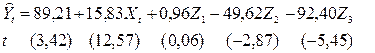
R² = 0,968; F = 59,76 > F_{0,05; 5; 8} = 3,69.

В этой модели почти все коэффициенты (дифференциальные свободные члены) статистически надежны на 5%-м уровне значимости (критическое значение t _{0,05; 8} = 2,31).

Итак, отдельные уравнения для каждого квартала:

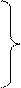
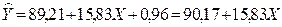- 1-й квартал,

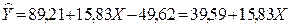- 2-й квартал,

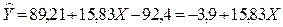- 3-й квартал,

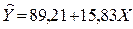- 4-й квартал.

На основе полученных уравнений можно прогнозировать величину рассматриваемого показателя в зависимости от цены с учетом сезонных изменений.

Дата добавления: 2015-08-20