Волны в плотных материалах

Прежде всего я напомню вам об удобном способе описания синусоидальных плоских волн, которым мы пользовались в гл. 36 (вып. 3). Любая компонента поля в волне (возьмем, на­пример, Е) может быть записана в форме

E=E₀e^i(wt-k•r), (33.6)

где Е — амплитуда поля в точке г (относительно начала коор­динат) в момент t. Вектор k указывает направление распростра­нения волны, а его величина | k |=k=2pl равна волновому числу. Фазовая скорость волны v_фаз=w/k для света в материале с показателем n будет равна c/n, поэтому

k=wn/c. (33.7)

Предположим, что вектор k направлен по оси z; тогда k•r будет просто хорошо знакомым нам kz. Для вектора k в любом другом направлении z следует заменить на r_k — расстояние от начала в направлении вектора k, т. е. kz мы должны заменить на kr_k, что как раз равно k•r (фиг. 33.2).

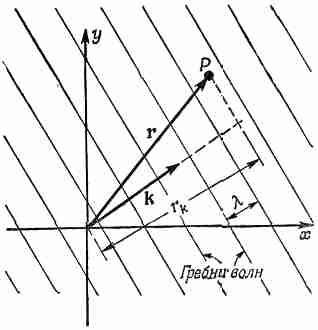
Фиг. 33.2. Фаза волны в точке Р, распространяющейся в направ­лении k, равна (wt- k • r ).

Таким образом, запись (33.6) является удобным представлением волны, идущей в любом направлении.

Разумеется, при этом мы должны помнить, что

k • r =k_xx+k_yy+k_:zz,

где k_x, k_y и k_z — компоненты вектора k по трем осям. Мы уже отмечали однажды, что на самом деле величины (w, k_x, k_y, k_z) образуют четырехвектор и что его скалярное произведение на (t, x, у, z) является инвариантом. Таким образом, фаза волны есть инвариант и формулу (33.6) можно записать в виде

Однако сейчас нам такие хитрости не понадобятся.

Для синусоидального по­ля Е, подобного выражению (33.6), производная dE/дt — это то же самое, что и iwE, a дЕ/дх — то же, что и ik_x E, и аналогично для остальных компо­нент. Вы видите, чем удобна форма (33.6): когда мы работаем с дифференциальными уравнениями, то дифференцирование заменяется простым умножением. Другое полезное качество состоит в том, что операция Ñ =(д/дx), (д/ду), (д/дz) заменяется тремя умножениями (- ik_x,-ik_y, -ik_z). Но эти три множителя преобразуются как компоненты вектора k, так что оператор Ñ заменяется умножением на

Правило остается справедливым для операции Ñ в любой ком­бинации, будь то градиент, дивергенция или ротор. Например, z-компонента ÑX Е равна

Если и Е_у и Е_х изменяются как e^{-i k•r} , то мы получаем

-ik_xE_y+ik_yE_x,

что представляет, как вы видите, z-компоненту —i k X Е.

Таким образом, мы получили очень полезный общий закон, что в любом случае, когда вам нужно взять градиент от вектора, который изменяется, как волна в трехмерном пространстве (а они в физике играют важную роль), эту операцию вы можете проделать быстро и почти без всяких раздумий, если вспомните, что оператор Ñ эквивалентен умножению на —i k.

Например, уравнение Фарадея

ÑX Е = д B / д t

превращается для волны в

— i k X Е =-iw B. Оно говорит, что

В = k X E /w. (33.9)

Это соответствует результату, найденному ранее для волн в пу­стом пространстве, т. е. что вектор В в волне направлен под прямым углом к вектору Е и направлению распространения волны. (В пустом пространстве w/k=с.) Знак в уравнении (33.9) вы можете проверить, исходя из того, что k является на­правлением вектора Пойнтинга S =e₀c²(E X В).

Если вы примените то же самое правило к другим уравне­ниям Максвелла, то снова получите результаты последней главы, в частности

Но раз уже это известно нам, давайте не будем проделывать все сначала.

Если вы хотите поразвлечься, можете попытаться решить та­кую устрашающую задачу (в 1890 г. она предлагалась студен­там на выпускных экзаменах): решите уравнения Максвелла для плоской волны в анизотропном кристалле, т. е. когда поля­ризация Р связана с электрическим полем Е через тензор поля­ризуемости. Конечно, в качестве ваших осей вы выберете глав­ные оси тензора, так что связи при этом упростятся (тогда Р_х=a_aЕ_х, Р_у=a_bЕ_у, a P_z=a_cE_z), но направление волны и ее поляризация пусть останутся произвольными. Вы должны найти соотношение между Е и В и определить, как изменяется k с направлением распространения волны и ее поляризацией. После этого вам будет понятна оптика анизотропного кристалла. Лучше начать с более легкого случая дважды лучепреломляющего кристалла, подобного турмалину, для которого два коэффи­циента поляризуемости равны между собой (например, a_b=a_c), и попытаться понять, почему, когда мы смотрим через такой кристалл, мы видим два изображения. Если это вам удастся, тогда испытайте свои силы на более трудном случае, когда все три а различны. После этого вам уже будет ясен уровень ваших знаний — знаете ли вы столько же, сколько студент, заканчи­вавший университет в 1890 г. Но мы с вами в этой главе будем рассматривать только изотропные вещества.

Из опыта вам известно, что когда на границу раздела двух материалов, скажем воздуха и стекла или воды и бензина, попадает плоская волна, то возникают как отраженная, так и преломленная волны.

Предположим, что, кроме этого факта, нам больше ничего неизвестно, и посмотрим, что можно из него вывести. Выберем наши оси так, чтобы плоскость yz совпадала с поверхностью раздела, а плоскость ху была перпендикулярна фронту волны (фиг. 33.3).

Фиг. 33.3. Векторы, распространения k, k' и k" для падающей, отраженной и прелом­ленной волн.

Электрический вектор в падающей волне может быть записан в виде

Поскольку вектор k перпендикулярен оси z, то

k•r =k_xx+k_yy. (33.12) Отраженную волну мы запишем как

так что ее частота равна w', волновое число k', а амплитуда Е' ₀. (Мы, конечно, знаем, что частота и величина вектора k в отра­женной волне те же, что и в падающей волне, но не хотим пред­полагать даже это. Пусть это все получится само собой из мате­матического аппарата.) Наконец, запишем преломленную волну:

Вы знаете, что одно из уравнений Максвелла дает соотноше­ние (33.9), так что для каждой из волн

Кроме того, если показатели преломления двух сред мы обозна­чим через n₁ и n ₂, то из уравнения (33.10) получится

Поскольку отраженная волна находится в том же ма­териале, то

в то время как для преломленной волны

Дата добавления: 2015-08-20