You must write detailed answers and explanations to all tasks and questions.

Position during the work.

During the exam students must take their places according to the following arrangement:

Group A – take their seats in the front part of the room (close to the board)

Group B – take their seats in the middle of the room

Group C – take their seats in the rear part of the room

Those who are not in the lists are regarded as students of group A.

Students, not taken the prescribed seat, are not allowed to start the exam.

Group “A”

Артамонов Михаил Сергеевич

Ахметгалиева Карина Рашитовна

Габриелян Ованес Рачиевич

Гордеева Кристина Олеговна

Гусева Екатерина Игоревна

Дейкун Елизавета Юрьевна

Евсеев Алексей Владимирович

Егоров Владислав Павлович

Зейналов Ариф Тагиевич

Илларионов Дмитрий Михайлович

Каратушин Павел Юрьевич

Киселев Артемий Вячеславович

Лиходедова Анна Петровна

Меджидова Айтан

Мутавчи Ксения Аркадьевна

Насыров Олег Олегович

Новиков Иван Владиславович

Сергеев Яков Данилович

Тихомиров Максим Сергеевич

Трошин Дмитрий Игоревич

Шарапов Михаил Михайлович

Group “B”

Антонов Денис Сергеевич
Бабушкин Михаил Васильевич
Баранова Мария Александровна
Буденкова Евгения Алексеевна
Буденкова Марина Алексеевна
Докучаев Алексей Михайлович
Ермилов Дмитрий Сергеевич
Жилина Юлия Сергеевна
Каджемонян Александр Аркадьевич
Мартазанов Ахмед Арсамакович
Мейльман Евгения Анатольевна
Помбрик Маргарита Вадимовна
Савельева Анастасия Александровна
Савостин Дмитрий Сергеевич
Самойленко Владислав Анатольевич
Самохвалова Татьяна Владимировна
Сарычев Никита Сергеевич
Слизков Антон Евгеньевич
Ходурский Даниил Михайлович
Цветкова Инесса Олеговна
Group “C”
Галибов Дмитрий Олегович
Грачева Анастасия Вячеславовна
Грибов Денис Константинович
Григорьева Анастасия Геннадьевна
Гургенидзе Николетта Шалвовна
Джамшедов Сиёвуш
Забелич Глеб Александрович
Иванчин-Писарева Александра
Картавов Игорь Владимирович
Квашнина Алина Игоревна
Кузнецов Михаил Константинович
Кумар Рохан Манодж
Лагутина Анастасия Юрьевна
Лактионова Ксения Александровна
Лудковская Анастасия Олеговна
Лукашенко Елена Сергеевна
Носкова Валерия Анатольевна
Пудова Дарья Олеговна
Самедова Аида Физулиевна
Сегал Олег Олегович
Тертышная Екатерина Сергеевна
Фам Данг Зиеу Ань
Циклаури Георги Шотаевич
Шаповалов Дмитрий Викторович

Full list of theoretical questions for the midterm attestation control work

(Your variant will contain exactly one question from this list. All your answers and solutions must be provided with detailed explanations! These questions are taken from the main textbook and have been explained during the lectures)

1. For the 2x2 matrices A,B,C their determinants |A| = 1, |B| = -3, |C| = 4. What is the determinant of the matrix A(B+C)? Why? Explain in details.

2. Which two of the following three conditions are equivalent:

a) The system Ax = 0 has only the trivial solution

b) det(A) = 0

c) Matrix A is invertible.

Explain in details.

3. Suppose that matrix B is invertible. Prove: AB ־ ¹ =B ־ ¹A if and only if AB=BA.

4. Prove that if {a,b,c} is linearly dependent set of vectors in a vector space V, and d is any vector in V, then { a,b,c,d } is also linearly dependent.

5. Prove, that if , then the reduced row-echelon form of

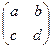is .

6. Prove the following theorem:

Any square matrix B can be represented in the form B=S+A, where S is symmetric, and A is anti-symmetric matrices. This representation is unique.

7. Give an example of inconsistent linear system, which has more unknowns than equations.

8. Give an example of 2x2 matrices A and B such that

9. Prove that, if A and B are square matrices such that , then

10. Let A be a square matrix, and I be identity matrix. Prove that for any natural number n

, if

11. Suppose that A and B are nxn matrices. Prove that

tr(AB) = tr(BA)

12. Let u, v, and w be nonzero vectors in 3-space with the same initial point, but such that no two of them are collinear. Prove that the vector u x(v x w) lies in the plane determined by v and w. Here the sign “x” denotes cross product.

13. Prove the Cauchy’s inequality, i.e. the absolute value of the inner product is not greater, than the product of the norms: |(u,v)| ≤||u||∙||v||

14. Prove the generalized theorem of Pythagoras: if the vectors u and v are orthogonal, then ||u+v||² = ||u||² + ||v||²

15. Prove the triangle inequality in inner product space: ||u+v|| ≤ ||u|| +||v||

16. Prove the “parallelogram equality”: ||u+v||² + ||u-v||² = 2||u||² + 2||v||²

17. Suppose that for a linear system Ax = b we have rank(A) = 4 and rank(A|b) = 5, where (A|b) is the augmented matrix. Is the system consistent? Why?

18. Recall that that the trace of a square matrix A is the sum of the elements on the main (principal) diagonal. Prove that the characteristic equation of a 2 2 matrix A can be expressed as

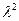-tr(A) 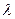+det(A)=0,

where tr(A) is the trace of A.

19. Prove that if a vector u is orthogonal to both vectors v and w, then u is orthogonal to av+bw for all scalars a and b.

20. Find , if is a positive integer and

.

21. Let

Show:

a) is diagonalizable, if .

b) is not diagonalizable, if .

22. Show that if is any matrix, then has an orthonormal set of eigenvectors.

23. Prove: if 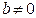, then the matrix

is not diagonalizable.

24. Use the Cayley-Hamilton theorem to calculate A 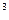for the matrix

. Explain the procedure in details.

25. Some 3x3 matrix A has the eigenvalues a= -2,b=2, c=3. Is the matrix A diagonalizable? Why?

Structure of the exam ticket.

The control work includes 7 tasks: 6 practical and 1 theoretical. Theoretical task is one of the questions listed above. For examples of the practical tasks, please look through your seminar and lecture note, and repeat corresponding parts of the textbook. A few samples are listed below.

1. Find the inverse of the matrix (if it’s invertible).

2. A task devoted to inner product of two vectors in Euclidian space.

Example. Suppose u,v, and w are vectors such that the inner products (u,v) = 3, (v,w) = -5, (u,w) = 7, and the norms | |u|| = 2, ||v|| = 4, ||w|| = 6. Evaluate the expression: (3u-v-2w,3u+2v+w).

Example. Use inner product to find the angle A in the triangle ABC with the vertices A(-1;3,-2), B(-2;-1,-3), C(7;-3,-4)

3. A task related to cross or triple vector product.

Example. Vectors and are given. Find the third vector , so that { 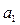, , } form an orthogonal basis in . Normalize the vectors , , and get the orthonormal basis { , , }.

Example. Use cross product to find the sine between vectors u=(1;2;3) and v=(3;2;1).

Example. Find the volume of parallelepiped with sides u, v, w:

u = (1;4;2), v = (3;2;1), w = (-2;4;6)

Example. Use cross product to find a general equation of the plane that passes through the straight lines:

and 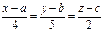. Here a,b,c – some constants.

4. Geometric task.

Example. Find an equation for the plane that passes through the point (1;-7;-8) and is parallel to the plane 2x-5y+3z-6=0.

Example. Find a general equation of the line in the 2-space that passes through the points A(3;1) and B(6;5)

Example. Find an equation of a straight line in R 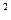that contains the point A =(1,2) and is orthogonal to the line passing through the points B =(0,3) and C =(-5,0).

Example. Find an orthogonal projection H of the point A(1;3) on the line

5x - 2y + 4 = 0

5. For the given matrix, find eigenvalues and bases for the eigenspaces.

Example.

Solution (in Russian).

Чтобы найти собственные значения матрицы , решаем характеристическое уравнение , т.е. . Последовательно получаем, что 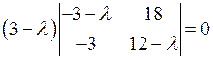, , . Поэтому собственными значениями матрицы являются 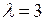и .

Найдем соответствующие собственные векторы. При 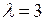характеристическая матрица принимает вид 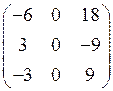. Решая соответствующую систему однородных уравнений, получим . Общее решение системы . Если то 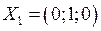, а если то , и множество собственных векторов, соответствующих собственному значению 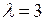, может быть записано в виде .

При получим систему ~ ~ , т.е. и 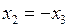, 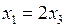. Общее решение системы . Таким образом, множество собственных векторов, соответствующих собственному значению , записывается в виде .

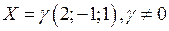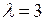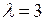
Ответ: Собственные значения и . При , при 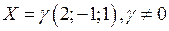. Векторы (0;1;0), (3;0;1) образуют базис (двумерного) собственного подпространства, соответствующего собственному значению 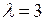. Вектор (2;-1;1) образует базис (одномерного) собственного подпространства, соответствующего собственному значению .

6. Diagonalization of non-symmetric and symmetric matrices.

Example. Determine, whether the matrix is diagonalizable. If so, find a matrix that diagonalizes and determine . See Set 6.2 exercises 9-14.

Example. Find a matrix that orthogonally diagonalizes and determine .

See set 6.3 exercises 2-9.

7. One theoretical question from the “Full list of theoretical questions for the midterm attestation control work”.

---

Дата добавления: 2015-08-03