Мощность множества

Аналогом понятия «количество элементов конечного множества» в случае бесконечного множества является понятие «мощность» множества.

Определение

Говорят, что два множества и имеют одинаковое число элементов или одинаковую мощность, если между их элементами может быть установлено взаимно однозначное соответствие.

Из данного определения следует, что множество натуральных чисел 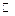содержит столько же элементов, сколько и множества чётных или нечётных чисел. Действительно, каждому натуральному числу сопоставим чётное число 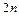или нечётное число .

Таким образом, для бесконечных множеств известный принцип Аристотеля «часть меньше целого» уже не является справедливым. В смысле сделанного определения часть может быть равна целому!

Возможность для множества быть равномощным своей части является характерным признаком бесконечных множеств. По Дедекинду множество называется конечным, если оно не равномощно никакому своему собственному подмножеству; в противном случае множество называется бесконечным.

Пример 1. Показать, что на гипотенузе прямоугольного треугольника точек «столько же», сколько и на катете.

Доказательство очевидно из рисунка. Достаточно спроектировать точки гипотенузы на соответствующий катет. Однако стоит помнить, что мощность множества и длина – это различные понятия, из совпадения мощностей множеств не вытекает равенство длин катета и гипотенузы.

Пример 2. Доказать равномощность интервала действительных чисел и множества действительных чисел

В данном случае проще непосредственно указать закон, задающий взаимнооднозначное отображение. Например, .

Определение

Множество, равномощное множеству натуральных чисел, называется счётным.

Согласно данному определению множество счётно, если оно содержит бесконечно много элементов, и притом все они могут быть расположены в виде последовательности, занумерованной натуральными числами.

Справедливы следующие леммы:

1. Любое бесконечное множество содержит счётное подмножество.
2. Любое бесконечное подмножество счётного множества счётно.

Из последнего утверждения следует, что мощность счётного множества – наименьшая бесконечная мощность.

Теорема о счётности множества рациональных чисел

Множество рациональных чисел счётно.

Доказано, что множество всех многочленов с рациональными коэффициентами счётно, множество всех точек на плоскости, у которых обе координаты рациональны: , счётно, множество алгебраических чисел (каждое из которых есть корень некоторого многочлена с целыми коэффициентами) также счётно.

Однако не все бесконечные множества являются счётными, подобные множества называются, естественно, несчётными.

Теорема Кантора о несчётности множества вещественных чисел

Множество вещественных чисел не является счётным.

Из теоремы Кантора непосредственно следует существование трансцендентных чисел (чисел, не являющихся алгебраическими), ибо если бы все вещественные числа были бы алгебраическими, то множество было бы счётным.

Пример 3. Установить взаимнооднозначное соответствие между открытым интервалом действительных чисел и полуинтервалом

В каждом множестве выделим множество чисел, образующихгеометрическую прогрессию: Для элементов и не принадлежащих и отличных от 0, установим тождественное отображение: Затем рассмотрим две последовательности и ; . Рассмотрим соответствие: Оно и является искомым: соответствует

Пример 4. Установить взаимно однозначное соответствие между точками, лежащими на стороне квадрата с вершинами , и всеми точками квадрата.

Для любой точки данного квадрата имеем: , т.е. , причём можно представить как . Поставим любой точке в соответствие число , принадлежащее отрезку . Таким образом, рассматриваемый квадрат и отрезок равномощны.

Дата добавления: 2015-07-25