
|
Читайте также: |
19.1. Монотонность: убывание и возрастание.
Напомним данное в пункте 15.2 определение монотонности функции 
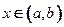 :
:
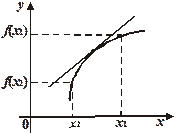
1) возрастания; 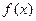 возрастает в интервале возрастает в интервале  , если , если 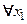 , , 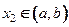
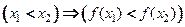
| 2) убывание; 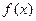 убывает в интервале убывает в интервале  , если , если 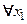 , , 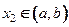
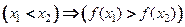
|
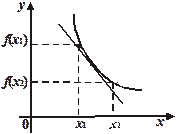
Рис. 19.1. Рис. 19.2.
Теорема 19.1. (Достаточные условия монотонности)
Пусть функция  дифференцируема в интервале
дифференцируема в интервале  .
.
1) Если 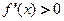 в каждой точке интервала
в каждой точке интервала  , то функция
, то функция  возрастает в интервале
возрастает в интервале  .
.
2) Если 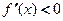 в каждой точке интервала
в каждой точке интервала  , то функция
, то функция  убывает в интервале
убывает в интервале  .
.
Доказательство: Пусть две точки 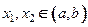 и
и 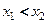 . Тогда по теореме Лагранжа (см. теорему 18.5) существует точка
. Тогда по теореме Лагранжа (см. теорему 18.5) существует точка 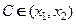 такая, что
такая, что
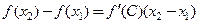 .
.
Так как 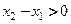 , то разность
, то разность 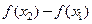 имеет тот же знак, что и
имеет тот же знак, что и 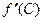 . Если
. Если 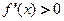 в интервале
в интервале  , в частности
, в частности 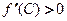 , то
, то 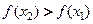 и функция
и функция  возрастает в интервале
возрастает в интервале  . Если
. Если 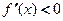 в интервале
в интервале  , в частности
, в частности 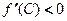 , то
, то 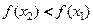 и
и 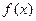 убывает в интервале
убывает в интервале  .
.
Теорема доказана.
Вывод: участки возрастания функции  находятся из решения неравенства
находятся из решения неравенства 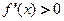 , а участки убывания – из неравенства
, а участки убывания – из неравенства 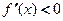 .
.
Установленная связь между знаком производной и направлением изменения функции геометрически ясна, если вспомнить, что производная функции в данной точке есть угловой коэффициент касательной к графику функции в этой точке. Знак этого углового коэффициента показывает, наклонена ли касательная вверх или вниз, а с нею идет ли верх (возрастает) или вниз (убывает) и сама кривая (рис. 19.1 и 19.2).
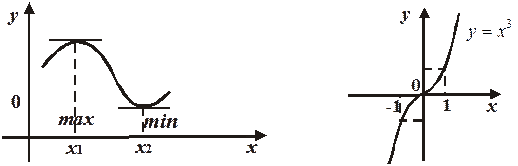
19.2. Экстремумы: максимумы и минимумы.
Особый интерес представляют точки, в которых меняется характер монотонности. Это точки максимума и минимума функции. Дадим необходимые определения.
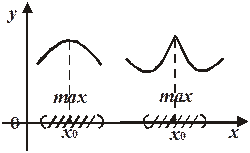
Точка  называется точкой максимума функции
называется точкой максимума функции  , если существует такая
, если существует такая 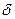 - окрестность
- окрестность 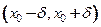 точки
точки  , что для всех
, что для всех 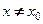 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 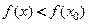 (см. рис. 19.3).
(см. рис. 19.3).
Рис. 19.3. Рис. 19.4.
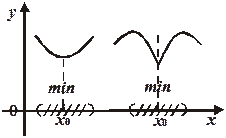 |
 Точка
Точка  называется точкой минимума функции
называется точкой минимума функции  , если существует такая
, если существует такая 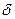 - окрестность
- окрестность 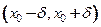 точки
точки  , что для всех
, что для всех 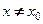 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 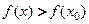 (см. рис. 19.4).
(см. рис. 19.4).
Замечание функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимумы и минимумы функции называются экстремумами функции.
Понятие экстремума связано с определенной окрестностью данной точки, т.е. носит локальный характер. Функция может иметь экстремум лишь во внутреннейточке области определения.
Из определения следует, что точка  - точка максимума (минимума) функции
- точка максимума (минимума) функции  тогда и только тогда, когда
тогда и только тогда, когда 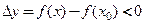
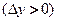 для всех
для всех 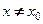 из некоторой окрестности точки
из некоторой окрестности точки  .
.
Теорема 19.2. (необходимое условие экстремума). Если функция  имеет в точке
имеет в точке  экстремум и дифференцируема в этой точке, то
экстремум и дифференцируема в этой точке, то  .
.
Доказательство: Так как в точке  функция
функция  имеет экстремум, то существует такая окрестность
имеет экстремум, то существует такая окрестность 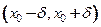 , в которой значение функции
, в которой значение функции 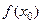 является наибольшим или наименьшим в указанной окрестности. По теореме Ферма (теорема 18.3) тогда
является наибольшим или наименьшим в указанной окрестности. По теореме Ферма (теорема 18.3) тогда  .
.
Теорема доказана.
Точки, в которых  , называются стационарными точками функции, в них приращается изменение функции, а касательная к графику в стационарной точке горизонтальна (параллельна оси
, называются стационарными точками функции, в них приращается изменение функции, а касательная к графику в стационарной точке горизонтальна (параллельна оси 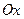 ) (см. рис. 19.5 и 19.6).
) (см. рис. 19.5 и 19.6).
 |
Точки, в которых производная не существует или равна нулю (стационарные точки), называются критическимиточками функции.
Итак, точки возможного экстремума непрерывной функции следует искать среди ее критических точек.
Как показывает пример функции 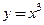 , точка
, точка 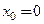 является ее стационарной точкой, т.к.
является ее стационарной точкой, т.к. 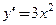 и
и 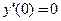 , но экстремума в точке
, но экстремума в точке 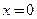 функция
функция 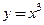 не имеет (см. рис. 19.6).
не имеет (см. рис. 19.6).
Теорема 19.3. (первое достаточное условие экстремума). Если непрерывная функция  дифференцируема в некоторой окрестности критической точки
дифференцируема в некоторой окрестности критической точки  и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная 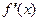 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то  - точка максимума; с минуса на плюс, то
- точка максимума; с минуса на плюс, то  - точка минимума.
- точка минимума.
Доказательство: Рассмотрим 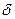 - окрестность
- окрестность 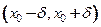 точки
точки  . Если
. Если 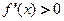 для всех
для всех  и
и 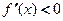 для всех
для всех 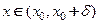 . Тогда функция
. Тогда функция  возрастает слева от точки
возрастает слева от точки  и убывает справа от точки
и убывает справа от точки  и убывает справа от точки
и убывает справа от точки  . Поэтому значение
. Поэтому значение 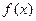 в точке
в точке  является наибольшим в интервале
является наибольшим в интервале 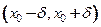 , т.е.
, т.е. 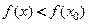 для всех
для всех 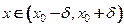 . Это и означает, что
. Это и означает, что  - точка максимума функции.
- точка максимума функции.
 | 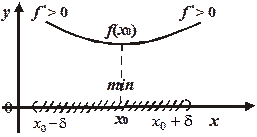 | ||
Аналогично доказывается и второй случай.
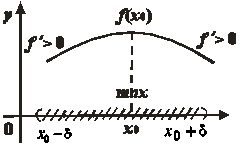
Графическая интерпретация доказательства теоремы 19.3 представлена на рисунке 19.7, а полученный результат изобразим в виде схемы:  - точка возможного условного экстремума, тогда
- точка возможного условного экстремума, тогда
 | 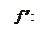 | ||||
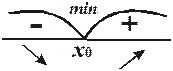 | |||||
Схема исследования функции на экстремум:
1) найти критические точки функции  ;
;
2) Выбросить из них лишь тепломассообменных, которые являются внутренними точками области определения функции;
3) исследовать знак производной 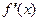 слева и справа от каждой из выбранных критических точек;
слева и справа от каждой из выбранных критических точек;
4) выбрать точки экстремума и вычислить значения функции в этих точках.
Теорема 19.4. (второе достаточное условие экстремума).
Пусть функция  имеет первую производную
имеет первую производную 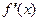 в окрестности стационарной точки
в окрестности стационарной точки  и вторую производную в самой точке
и вторую производную в самой точке  , при этом
, при этом 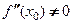 . Тогда
. Тогда
1) если 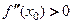 , то
, то  - точка минимума функции;
- точка минимума функции;
2) если 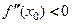 , то
, то  - точка максимума функции;
- точка максимума функции;
Доказательство: Запишем формулу Тейлора функции  в точке
в точке  . Согласно теореме 18.9. имеем:
. Согласно теореме 18.9. имеем:
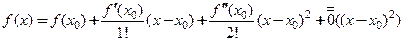 .
.
Учитывая, что  - стационарная точка, т.е.
- стационарная точка, т.е.  , для приращения аргумента в окрестности точки
, для приращения аргумента в окрестности точки  получим
получим
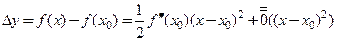
или, отбрасывая б.м. более высокого порядка, чем 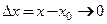 ,
,
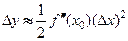 .
.
Это означает, что 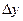 имеет тот же знак, что и
имеет тот же знак, что и 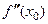 , в окрестности точки
, в окрестности точки  . Поэтому,
. Поэтому,
если 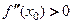 , то
, то 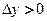 и
и  - точка минимума,
- точка минимума,
если 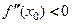 , то
, то 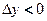 и
и  - точка максимума.
- точка максимума.
Дата добавления: 2015-07-20; просмотров: 173 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Некоторые приложения формулы Маклорена. | | | Наибольшее и наименьшее значения функции на отрезке. |