Решение. Повторный интеграл является следствием двойного, поэтому

Повторный интеграл является следствием двойного, поэтому

I = .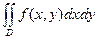

Для восстановления области D выписываем из данного повторного интеграла границы области:

y = -2, y = -1, x = , x = 0;

y = -1, y = 0, x = .

Построим линии, ограничивающие область.

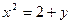, следовательно () – уравнение параболы с вершиной в точке (0,-2).

, следовательно () – уравнение параболы с вершиной в точке (0,0) (рис. 6).

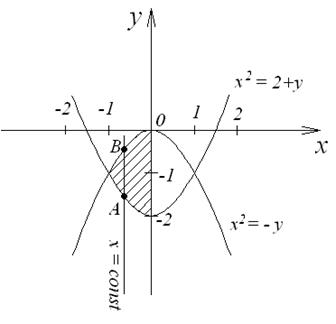
Рис. 6

Найдем точки пересечения парабол:

2 + y = – y,

2 y = – 2,

y = – 1.

Подставляем в

, но ,

значит .

Производим переход в двойном интеграле к повторному, при этом внешнее интегрирование производим по x, внутреннее – по y. Т.е. возьмем постоянные пределы по переменной x. Для этого спроецируем область D на ось Ox. Проекцией будет отрезок [– 1; 0]. Если провести прямую, параллельную оси Oy (x = const), то она пересекает область D в точках A (назовем ее точкой входа) и B (назовем ее точкой выхода).

Точка A лежит на параболе x² = y + 2 (т.е. y = x ² – 2). Точка B лежит на параболе (т.е. y = – x ²).

Получим I = ; и находим из уравнений соответствующих парабол:

1) точка A лежит на параболе x² = y + 2 (т.е. y = x ² – 2), значит, = x ² – 2;

2) точка B лежит на параболе (т.е. y = – x ²), значит = – x ².

Окончательно получим: I = .

Ответ: I = .

2. Вычислить двойной интеграл по области D, ограниченной заданными линиями. Сделать чертеж.

2.1. I = 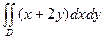, где область D, ограничена линиями y = x, y = 2 x, x = 2, x = 3.

2.2. I = , где область D, ограничена линиями 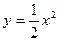, y = x.

Решение.

2.1. Изобразим область интегрирования D (рис. 7).

Рис. 7

Область интегрирования принадлежит к виду (4) (см. п.2), тогда

D: ,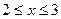

.

Вычислим искомый интеграл:

I = =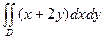

= = .

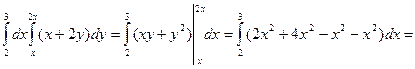
Ответ: .

2.2. Изобразим область интегрирования D (рис. 8).

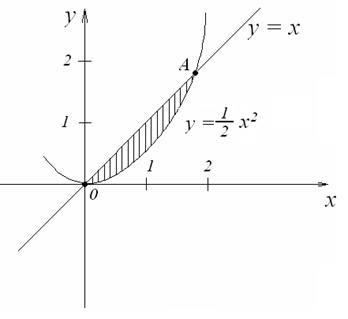
Рис. 8

Область интегрирования принадлежит к виду (4) (см. п.2).

Так как прямая y = x и парабола 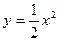пересекаются в точках O(0,0) и A(2,2), то область D определяется системой неравенств:

,

.

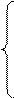Теперь вычислим искомый интеграл:

I = = =

= = ) = =

= .

;

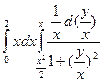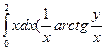
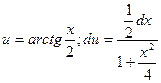Вычислим = =

dv = dx: v = x.

Применим формулу интегрирования по частям

(17)

= xarctg = =

= .

Итак, наш интеграл

I = 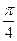2 .

Ответ: .

3. С помощью двойного интеграла вычислить площадь фигуры, ограниченной заданными линиями (сделать чертеж):

3.1. 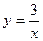, , 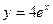y = 3, y = 4.

3.2. 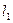: ; (18)

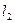: ; (19)

y = 0, y = x.

Дата добавления: 2015-07-20