
Читайте также:
|
|
 , проведенной в точке с абсциссой
, проведенной в точке с абсциссой  :
:
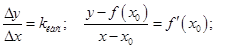
Определение. Нормалью к кривой в точке  кривой называется прямая, проходящая через точку
кривой называется прямая, проходящая через точку  , перпендикулярная касательной к кривой в этой точке.
, перпендикулярная касательной к кривой в этой точке.
 |
Замечание. Надеемся, что читатель помнит, как связаны угловые коэффициенты взаимно препендикулярных кривых. Все же напомним: 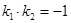 .
.
( )
)
Запишем уравнение нормали к графику функции  , проведенной в точке с абсциссой
, проведенной в точке с абсциссой  :
:
|

 Задание. 1) Написать уравнение касательной и нормали, проведенных к графику функции
Задание. 1) Написать уравнение касательной и нормали, проведенных к графику функции  в точке с абсциссой
в точке с абсциссой  .
.
а) 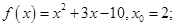 б)
б) 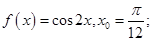
 в)
в) 
2) Написать уравнение всех касательных к графику функции 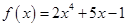 , проходящих через точку
, проходящих через точку  .
.
3) При каких значениях параметра  прямая
прямая  является касательной к графику
является касательной к графику 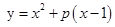 ?
?
4) Под каким углом синусоида 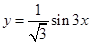 пересекает ось
пересекает ось 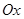 в начале координат?
в начале координат?
5) Найти длину отрезка касательной к кривой 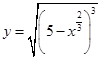 , проведенной через точку
, проведенной через точку  , заключенного между осями координат.
, заключенного между осями координат.
6) При каком значении  касательная к графику
касательная к графику  образует с осью абсцисс угол, равный
образует с осью абсцисс угол, равный 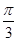 , и отсекает от 4-й четверти треугольник с площадью
, и отсекает от 4-й четверти треугольник с площадью 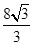 ?
?
7) Найти уравнения общих касательных к графикам 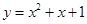 и
и 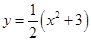 .
.
8) Найти наименьшее расстояние между графиками  и
и  .
.
9) В произвольной точке графика функции  проведена касательная. Доказать, что длина отрезка касательной от точки касания до пересечения с осью Oy равна ординате точки пересечения.
проведена касательная. Доказать, что длина отрезка касательной от точки касания до пересечения с осью Oy равна ординате точки пересечения.
10) Найти расстояние от точки  до параболы
до параболы 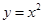 (наименьшее расстояние между точкой А и точкой параболы).
(наименьшее расстояние между точкой А и точкой параболы).
11) Найдите уравнение прямой, касающейся графика функции  в двух точках.
в двух точках.
Решения.
1) Написать уравнение касательной и нормали, проведенных к графику функции  в точке с абсциссой
в точке с абсциссой  : а)
: а) 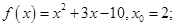 б)
б) 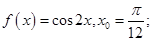 в)
в) 
а)  . Найдем производную функции
. Найдем производную функции  :
:  .
.  . Уравнение касательной:
. Уравнение касательной:  . В данном случае
. В данном случае  ; Ответ.
; Ответ. 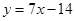 .
.
б)  .
. 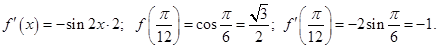
Уравнение касательной: 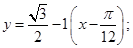 Ответ.
Ответ.  .
.
в) 

Уравнение касательной: 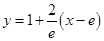 . Ответ.
. Ответ.  .
.
2) Написать уравнение всех касательных к графику функции 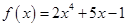 , проходящих через точку
, проходящих через точку  .
.
Задание отличается от предыдущего тем, что данная точка не является точкой касания, необходимой для записи уравнения. Поэтому абсциссу точки касания мы обозначим какой-либо буквой, например, 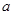 . Запишем уравнение касательной к графику данной функции в общем виде (с неизвестной абсциссой точки касания
. Запишем уравнение касательной к графику данной функции в общем виде (с неизвестной абсциссой точки касания 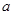 ):
): 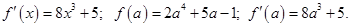
Уравнение касательной:  . Если точка
. Если точка  принадлежит касательной, то ее координаты
принадлежит касательной, то ее координаты  удовлетворяют записанному уравнению:
удовлетворяют записанному уравнению:  Осталось для каждого из найденных значений
Осталось для каждого из найденных значений 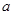 найти уравнение (подставив
найти уравнение (подставив 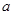 в приведенное выше уравнение
в приведенное выше уравнение  ).
).
Ответ. 
3) При каких значениях параметра  прямая
прямая  является касательной к графику
является касательной к графику 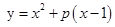 ?
?
Задание можно выполнить как методами 9-го класса, так и с применением производной.
I способ. Напишем уравнение касательной к данной квадратичной функции в общем виде, т.е. с неизвестной абсциссой точки касания 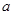 :
: 
Тогда по условию задачи  , т.е.
, т.е.  , и
, и 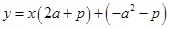 - одна и та же прямая, т.е. коэффициенты при
- одна и та же прямая, т.е. коэффициенты при  и свободные члены в данных уравнениях должны совпадать.
и свободные члены в данных уравнениях должны совпадать.
Получаем систему уравнений с двумя неизвестными (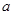 и
и  ):
):  . Решая систему, получаем искомые значения
. Решая систему, получаем искомые значения  .
. 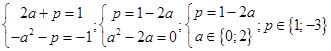 .
.
Ответ. 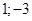 .
.
II способ. Воспользуемся другим определением касательной к параболе (подобное определение можно дать касательной к графику любой гладкой функции, обладающей выпуклостью только одного типа):
Прямая, не параллельная оси параболы, называется касательной, если она имеет с параболой единственную общую точку.
Задача свелась к вопросу: «При каких значениях параметра  уравнение
уравнение  имеет единственное решение?» Приравняем дискриминант к 0:
имеет единственное решение?» Приравняем дискриминант к 0: 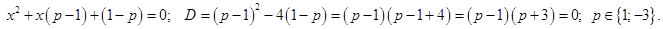
Ответ. 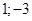 .
.
4) Под каким углом синусоида 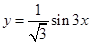 пересекает ось
пересекает ось 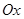 в начале координат?
в начале координат?
Угол между кривыми в точке их пересечения – это угол между касательными, проведенными к кривым в их общей точке.
Найдем угол наклона касательной к синусоиде 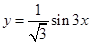 в начале координат. Тангенс угла – это значение производной функции
в начале координат. Тангенс угла – это значение производной функции 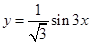 в точке
в точке  .
. 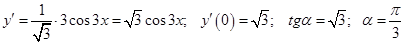 . Ответ.
. Ответ. 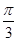 .
.
5) Найти длину отрезка касательной к кривой 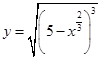 , проведенной через точку
, проведенной через точку  , заключенного между осями координат.
, заключенного между осями координат.
Напишем уравнение касательной к данному графику в общем виде с неизвестной абсциссой точки касания 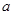 :
: 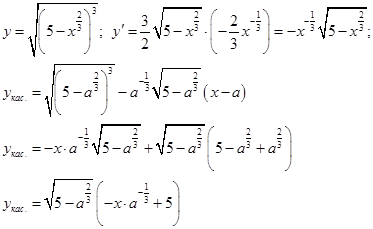
Запишем условие принадлежности касательной точки  :
: 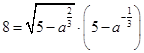 .
. 
Проверкой убеждаемся, что  - корень уравнения 2-й кратности.
- корень уравнения 2-й кратности. 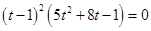 .
.
Уравнение 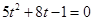 положительных корней не имеет. Т.о. абсцисса точки касания найдена –
положительных корней не имеет. Т.о. абсцисса точки касания найдена –  . Уравнение искомой касательной принимает вид
. Уравнение искомой касательной принимает вид  . Точки пересечения касательной с осями координат:
. Точки пересечения касательной с осями координат:  и
и  , а длина отрезка касательной, заключенного между осями координат равна
, а длина отрезка касательной, заключенного между осями координат равна  .
.
Ответ. 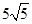 .
.
6) При каком значении  касательная к графику
касательная к графику  образует с осью абсцисс угол, равный
образует с осью абсцисс угол, равный 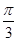 , и отсекает от 4-й четверти треугольник с площадью
, и отсекает от 4-й четверти треугольник с площадью 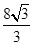 ?
?
Приведем два способа решения задачи.
I способ. Пусть абсцисса точки касания -  . Общий вид уравнения касательной –
. Общий вид уравнения касательной –
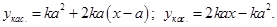
Первое условие – угол наклона 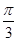 , т.е. угловой коэффициент касательной равен
, т.е. угловой коэффициент касательной равен  . Получаем уравнение
. Получаем уравнение  .
.
Точки пересечения касательной с осями координат:  и
и 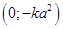 . Площадь треугольника
. Площадь треугольника  . Заметим, что по условию касательная должна отсекать треугольник от 4-й четверти, т.е.
. Заметим, что по условию касательная должна отсекать треугольник от 4-й четверти, т.е.  ,
,  .
.
Запишем и решим относительно  систему, полученную из условия задачи:
систему, полученную из условия задачи:  Ответ.
Ответ.  .
.
|
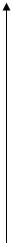 II способ. Начнем с уравнения прямой, угол наклона которой к оси Ох равен
II способ. Начнем с уравнения прямой, угол наклона которой к оси Ох равен 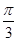 , а площадь треугольника, отсекаемого прямой от 4-й четверти, равна
, а площадь треугольника, отсекаемого прямой от 4-й четверти, равна 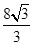 .
.
 |



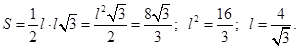
Уравнение прямой:  при
при 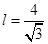 уравнение
уравнение
принимает вид 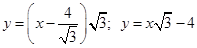 .
.
Поставим условие касания, т.е. единственности общей точки прямой и параболы (именно параболы, а не прямой 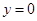 , - это следует из условия задачи).
, - это следует из условия задачи).
 Ответ.
Ответ.  .
.
7) Найти уравнения общих касательных к графикам 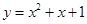 и
и 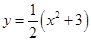 .
.
Приведем самый обычный и АБСОЛЮТНО НЕВЕРНЫЙ способ решения этой задачи, после применения которого обычно следуют жалобы на некорректное условие и отсутствие ответа (мы не хотим сказать, что все наши читатели обязательно стали бы делать так же):
 Запишем для каждой функции уравнение касательной в общем виде
Запишем для каждой функции уравнение касательной в общем виде 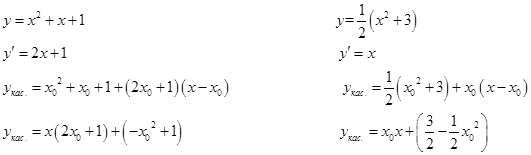 ,
,
после чего приравняем в правых частях соответствующие коэффициенты и найдем  :
:


 Почему же этот способ неверный? Ведь кажется, что все использованные ранее приемы проведены правильно! Дело в том, что общая касательная - это прямая, которая касается и того, и другого графика, но не обязательно в одной точке. (Для сравнения дадим другой вопрос: «Когда две параболы имеют единственную общую точку?» Правда, на этот вопрос легче отвечать без применения производной.)
Почему же этот способ неверный? Ведь кажется, что все использованные ранее приемы проведены правильно! Дело в том, что общая касательная - это прямая, которая касается и того, и другого графика, но не обязательно в одной точке. (Для сравнения дадим другой вопрос: «Когда две параболы имеют единственную общую точку?» Правда, на этот вопрос легче отвечать без применения производной.)
 Сравните:
Сравните:
 | |||
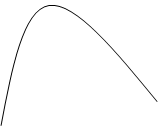 | |||
Общая касательная,
различные точки касания.
Общая касательная,
I способ. одна точка касания.
Теперь понятно, как исправить предыдущий способ решения. Пусть абсциссы касания искомой общей касательной с первым графиком - 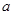 , со вторым -
, со вторым -  . Записываем дважды уравнение общей касательной:
. Записываем дважды уравнение общей касательной:  . Заметим, что для написания уравнения общей касательной достаточно найти из системы только
. Заметим, что для написания уравнения общей касательной достаточно найти из системы только 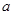 или только
или только  .
.
 .
.
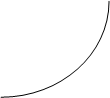
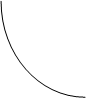 Получаем две общие касательные:
Получаем две общие касательные: 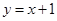 и
и  .
.

Ответ. 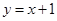 ;
;  .
.
| |||
 |
II способ. Пусть уравнение искомой общей касательной - 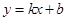 (с неопределенными коэффициентами). Запишем условие единственности общей точки с прямой для каждой параболы:
(с неопределенными коэффициентами). Запишем условие единственности общей точки с прямой для каждой параболы:

 Ответ.
Ответ. 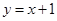 ;
;  .
.
8) Найти наименьшее расстояние между графиками  и
и  .
.
Первое, что необходимо сделать при решении данной задачи, -проверить, нет ли у графиков общих точек. Если есть, то ответом будет 0.
Решаем уравнение 

 Если бы одна из предложенных кривых не являлась прямой, то нам пришлось бы искать общую нормаль. Но здесь достаточно найти все касательные к первому графику, параллельные данной прямой, выбрать из них ближайшую к прямой и найти расстояние между касательной и данной прямой. На чертеже изобразим решение того же задания для КАКИХ-ЛИБО кривой и прямой:
Если бы одна из предложенных кривых не являлась прямой, то нам пришлось бы искать общую нормаль. Но здесь достаточно найти все касательные к первому графику, параллельные данной прямой, выбрать из них ближайшую к прямой и найти расстояние между касательной и данной прямой. На чертеже изобразим решение того же задания для КАКИХ-ЛИБО кривой и прямой:

Итак, найдем, в каких точках касательная к кривой  параллельна прямой
параллельна прямой  , т.е. имеет угловой коэффициент 2.
, т.е. имеет угловой коэффициент 2. 
В данном случае нам повезло – такая точка оказалась единственной (соответствующее уравнение касательной -  , т.е.
, т.е.  ). Все же выясним, как же выбрать из нескольких прямых, параллельных прямой
). Все же выясним, как же выбрать из нескольких прямых, параллельных прямой  , ближайшую к ней. Дело в том, что эти прямые отличаются только свободным членом. Нужно было бы выбрать свободный член, наиболее близкий к числу -4.
, ближайшую к ней. Дело в том, что эти прямые отличаются только свободным членом. Нужно было бы выбрать свободный член, наиболее близкий к числу -4.
А теперь – осторожно! Нужно найти расстояние между прямыми  и
и  . Ни в коем случае не пишем автоматически в ответ разность свободных членов, т.е.4. 4 – это расстояние на оси ординат между точками пересечения с ней данных прямых, а вовсе
. Ни в коем случае не пишем автоматически в ответ разность свободных членов, т.е.4. 4 – это расстояние на оси ординат между точками пересечения с ней данных прямых, а вовсе
не расстояние между прямыми!

 Предложим несколько способов решения этой задачи.
Предложим несколько способов решения этой задачи.
I способ. (Аналитический.) Написать уравнение любой
прямой, перпендикулярной данным, найти точки
пересечения ее с данными прямыми, найти расстояние
между этими точками.
|
нормали, проведенной к данной кривой в найденной
точке касания  (в данном случае, в начале
(в данном случае, в начале
координат), найти точку  ее пересечения с данной
ее пересечения с данной
в условии задачи прямой, вычислить расстояние 
между этой точкой и точкой касания.
В данном случае: нормаль - 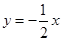 ;
; 
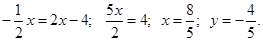
 .
.
 . Ответ.
. Ответ.  .
.
III способ. (Геометрический.) Из найденного ранее
в прямоугольном треугольнике  известен катет
известен катет  и острый угол
и острый угол  (он равен углу
(он равен углу
наклона 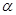 заданной прямой к оси абсцисс), тангенс которого равен 2. Тогда
заданной прямой к оси абсцисс), тангенс которого равен 2. Тогда
 . Ответ.
. Ответ.  .
.
IV способ. (Модификация предыдущего.)  ,
, 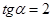 .
.
Тогда второй катет треугольника 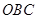
 ; высоту указанного прямоугольного
; высоту указанного прямоугольного
треугольника  получаем делением произведения катетов на гипотенузу:
получаем делением произведения катетов на гипотенузу:
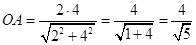 . Ответ.
. Ответ.  .
.
Заметим, что способ с нормалью удобен в том случае, когда нужно найти ближайшие
точки кривой и прямой, или же Вам не хочется делать чертеж.
9) В произвольной точке графика функции  проведена касательная. Доказать, что длина отрезка касательной от точки касания до пересечения с осью Oy равна ординате точки пересечения.
проведена касательная. Доказать, что длина отрезка касательной от точки касания до пересечения с осью Oy равна ординате точки пересечения.
Приведем два способа решения этой задачи: «честный», т.е. «для трудолюбивых», и
«быстрый», «для внимательных».
I способ. (Аналитический.)  ;
; 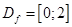 .
. 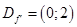 . Пусть
. Пусть  - абсцисса точки касания.
- абсцисса точки касания. 
Точка касания:  . Точка пересечения касательной с осью ординат:
. Точка пересечения касательной с осью ординат: 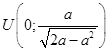 .
.
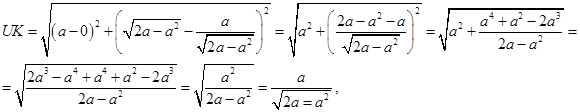
что и требовалось доказать.
II способ. (Графический.) Не начиная громоздких преобразований, построим график заданной функции.  Получили верхнюю полуокружность с центром в точке
Получили верхнюю полуокружность с центром в точке 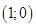 радиуса 1.
радиуса 1.
| 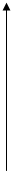 | |||

 Тогда получается, что в задаче просили просто доказать свойство
Тогда получается, что в задаче просили просто доказать свойство
равенства отрезков касательных, проведенных из одной точки
к одной и той же окружности! Задача решена.
 |
10) Найти расстояние от точки  до параболы
до параболы 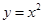 (наименьшее расстояние между точкой А и точкой параболы).
(наименьшее расстояние между точкой А и точкой параболы).
Во-первых, задачу можно решать как задачу на наименьшее значение. Но сейчас у нас речь идет о касательных и нормалях, поэтому переформулируем задание:
«Найти длину отрезка нормали к параболе 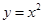 , проходящей через точку
, проходящей через точку  , от точки А до точки параболы.»
, от точки А до точки параболы.»
Пишем уравнение нормали в общем виде. (Абсцисса точки параболы, в которой проведена нормаль,  .)
.)
 Условие принадлежности точки А искомой нормали:
Условие принадлежности точки А искомой нормали: 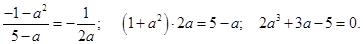 Один из корней полученного кубического уравнения легко угадывается: это
Один из корней полученного кубического уравнения легко угадывается: это  . Разделив многочлен
. Разделив многочлен  на
на  например, по схеме Горнера, для остальных корней получаем уравнение
например, по схеме Горнера, для остальных корней получаем уравнение
| -5 | |||
 , не имеющее действительных
, не имеющее действительных
корней. 1
Точка, в которой проведена нормаль, имеет координаты  . Искомое расстояние –
. Искомое расстояние –
это расстояние между точками  и
и  , т.е.
, т.е. 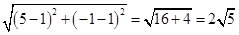 .
.
Ответ. 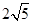 .
.
11) Найдите уравнение прямой, касающейся графика функции 
в двух точках.
Представьте себе, что мы для решения задачи напишем два (!) уравнения касательной с различными абсциссами точек касания 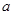 и
и  (!) к функции, заданной уравнением 4-й степени (!), а затем будем приравнивать коэффициенты при переменной и свободные члены (!). Представили? А теперь попробуем найти другой способ.
(!) к функции, заданной уравнением 4-й степени (!), а затем будем приравнивать коэффициенты при переменной и свободные члены (!). Представили? А теперь попробуем найти другой способ.
Что происходит при касании графика многочлена 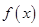 с прямой
с прямой 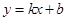 ? Кривая (график) и прямая имеют общую точку
? Кривая (график) и прямая имеют общую точку 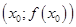 , т.е. уравнение
, т.е. уравнение  имеет корень
имеет корень  , но этот корень обязательно имеет кратность выше первой!
, но этот корень обязательно имеет кратность выше первой!
Например, в случае с касанием прямой и параболы парабола имеет с прямой общую точку, но при переходе через эту общую точку остается по ту же сторону от прямой, т.е. разность  не меняет знак при переходе через
не меняет знак при переходе через  . (Здесь
. (Здесь  - корень кратности 2.) Возникают ассоциации с решением неравенств методом интервалов? А кубическая парабола
- корень кратности 2.) Возникают ассоциации с решением неравенств методом интервалов? А кубическая парабола 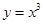 , имея касательную
, имея касательную 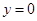 (в точке
(в точке 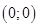 ), переходит с одной ее стороны на другую! (Здесь корень кратности 3.)
), переходит с одной ее стороны на другую! (Здесь корень кратности 3.)
Вернемся к нашей задаче. Пусть 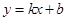 - искомая прямая. Тогда уравнение
- искомая прямая. Тогда уравнение  по условию задачи должно иметь два различных кратных корня. Степень уравнения – 4, т.о. оба корня должны быть 2-й кратности. Т.к. коэффициент при старшей степени переменной равен 1, можно записать следующее равенство с неопределенными коэффициентами (здесь
по условию задачи должно иметь два различных кратных корня. Степень уравнения – 4, т.о. оба корня должны быть 2-й кратности. Т.к. коэффициент при старшей степени переменной равен 1, можно записать следующее равенство с неопределенными коэффициентами (здесь  и
и 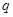 - вышеупомянутые кратные корни):
- вышеупомянутые кратные корни):  . Запишем систему на коэффициенты при соответствующих степенях переменной
. Запишем систему на коэффициенты при соответствующих степенях переменной  :
:  . Решаем систему из 1-х двух строк:
. Решаем систему из 1-х двух строк:  ;
;  .
.
Подставляем найденные  и
и 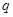 в последние две строки:
в последние две строки:  .
.
Получаем уравнение прямой  . Желающие могут проверить количество точек касания.
. Желающие могут проверить количество точек касания.
Ответ.  .
.
Задания для самостоятельного решения.
1) Напишите уравнения касательной и нормали, проведенных к графику функции  в точке с абсциссой
в точке с абсциссой  : а)
: а)  ; б)
; б) 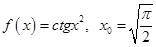 ;
;
 в)
в) 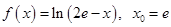 ; г)
; г) 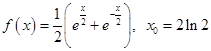 ; д)
; д)  .
.
2) Составьте уравнения касательных, проведенных из точки  к параболе
к параболе  . Найдите площадь треугольника АМВ, если А и В – точки касания.
. Найдите площадь треугольника АМВ, если А и В – точки касания.
3) Найдите угол между двумя касательными, проведенными из точки  к параболе
к параболе 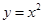 .
.
4) В какой точке кривой 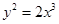 касательная перпендикулярна прямой
касательная перпендикулярна прямой  ?
?
5) При каких  касательные к графикам функций, проведенные в точках с абсциссой
касательные к графикам функций, проведенные в точках с абсциссой  , параллельны? а)
, параллельны? а) 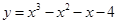 и
и 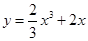 ; б)
; б)  и
и 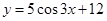 .
.
6) 
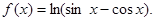 В каких точках касательная к графику этой функции параллельна оси Ох?
В каких точках касательная к графику этой функции параллельна оси Ох?
7) Прямая  является касательной к графику
является касательной к графику  . Найти координаты точки касания.
. Найти координаты точки касания.
8) Докажите, что при любом значении 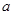 существует касательная к графику
существует касательная к графику 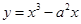 , перпендикулярная к прямой
, перпендикулярная к прямой  .
.
9) Вычислите площадь треугольника, ограниченного осями координат и касательной к графику функции 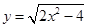 в точке с абсциссой
в точке с абсциссой 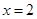 .
.
10) Докажите, что площадь треугольника, ограниченного осями координат и произвольной касательной к графику функции  , равна 2.
, равна 2.
11) При каких 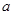 какие-либо из касательных, проведенных к графику функции
какие-либо из касательных, проведенных к графику функции 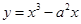 в точках пересечения этого графика с осью абсцисс, пересекаются под углом
в точках пересечения этого графика с осью абсцисс, пересекаются под углом 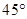 ?
?
12) Найдите уравнение параболы 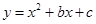 , касающейся прямой
, касающейся прямой  в точке
в точке  .
.
13) Найдите все действительные значения параметра 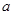 , при которых график функции
, при которых график функции  касается оси абсцисс.
касается оси абсцисс.
14) Из некоторой точки графика функции  касательная наклонена к оси абсцисс под углом
касательная наклонена к оси абсцисс под углом 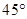 . Вычислить площадь фигуры, ограниченной этой касательной и прямыми
. Вычислить площадь фигуры, ограниченной этой касательной и прямыми  .
.
15) Найдите уравнение прямой, проходящей через точку 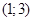 , касающейся графика
, касающейся графика 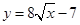 и пересекающей в двух различных точках график
и пересекающей в двух различных точках график 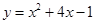 .
.
16) Найдите уравнение прямой, проходящей через точку 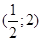 , касающейся графика
, касающейся графика 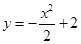 и пересекающей в двух различных точках график
и пересекающей в двух различных точках график 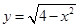 .
.
17) Найдите площадь треугольника, отсекаемого от координатных осей касательной к кривой 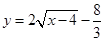 , проведенной параллельно прямой
, проведенной параллельно прямой  .
.
18) Найдите точку пересечения касательной к графику функции  в точке с абсциссой
в точке с абсциссой  и наклонной асимптоты графика функции
и наклонной асимптоты графика функции  .
.
19) При каких 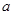 и
и  парабола
парабола  касается прямых
касается прямых  и
и 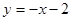 ?
?
20) При каких  из точки
из точки 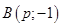 можно провести три различные касательные к графику функции
можно провести три различные касательные к графику функции  ?
?
21) Составьте уравнения всех общих касательных к параболам: а)  и
и 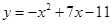 ; б)
; б)  и
и 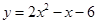 .
.
22) Составьте уравнение касательной к графику  , параллельной прямой
, параллельной прямой  . Найдите расстояние между касательной и данной прямой.
. Найдите расстояние между касательной и данной прямой.
23) Найдите такие точки А (на графике функции 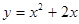 ) и В (на графике функции
) и В (на графике функции 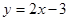 ), расстояние между которыми наименьшее.
), расстояние между которыми наименьшее.
24) К графику функции  проведена касательная в той точке 2-й четверти, где угловой коэффициент равкен 3. Найдите точки пересечения этой касательной с координатными осями.
проведена касательная в той точке 2-й четверти, где угловой коэффициент равкен 3. Найдите точки пересечения этой касательной с координатными осями.
25) На графике функции  найти все такие точки, что касательная к этому графику в искомых точках отсекает от положительной полуоси
найти все такие точки, что касательная к этому графику в искомых точках отсекает от положительной полуоси 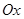 вдвое меньший отрезок, чем от отрицательной полуоси
вдвое меньший отрезок, чем от отрицательной полуоси 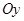 . Определить длины отсекаемых отрезков.
. Определить длины отсекаемых отрезков.
26)  Напишите уравнение касательной к графику данной функции, образующей с осями координат равнобедренный прямоугольный треугольник. а)
Напишите уравнение касательной к графику данной функции, образующей с осями координат равнобедренный прямоугольный треугольник. а)  ; б)
; б)  .
.
27) При каком значении 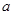 касательная к графику функции
касательная к графику функции 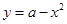 отсекает от первой четверти равнобедренный прямоугольный треугольник с площадью, равной
отсекает от первой четверти равнобедренный прямоугольный треугольник с площадью, равной  ?
?
28) Найдите все такие значения 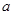 , при которых касательная к графику функции
, при которых касательная к графику функции 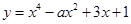 , проведенная в его точке с абсциссой 1, имеет с этим графиком ровно одну общую точку.
, проведенная в его точке с абсциссой 1, имеет с этим графиком ровно одну общую точку.
29) Покажите, что у астроиды 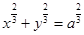 отрезок касательной, содержащийся между координатными осями, имеет постоянную величину, равную
отрезок касательной, содержащийся между координатными осями, имеет постоянную величину, равную 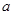 .
.
30) Найдите общие точки графика функции 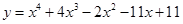 и прямой
и прямой  . В каких из них прямая является касательной к графику?
. В каких из них прямая является касательной к графику?
31) Найдите уравнения всех тех касательных к графику функции 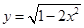 , каждая из которых вместе с осями координат ограничивает треугольник площадью
, каждая из которых вместе с осями координат ограничивает треугольник площадью  .
.
32) На прямой 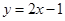 найдите все такие точки, что через каждую из них проходят ровно две касательные к графику функции
найдите все такие точки, что через каждую из них проходят ровно две касательные к графику функции 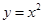 , а угол между этими касательными равен
, а угол между этими касательными равен  .
.
33) Существует ли касательная к графику функции  , имеющая с ним ровно две общие точки? Если да, то напишите ее уравнение.
, имеющая с ним ровно две общие точки? Если да, то напишите ее уравнение.
34) Найдите все отрицательные 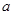 , для каждого из которых касательные к параболе
, для каждого из которых касательные к параболе  , проведенные через точку оси
, проведенные через точку оси 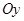 с ординатой
с ординатой 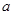 , высекают на оси
, высекают на оси 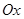 отрезок длины 4.
отрезок длины 4.
35) Укажите координаты всех точек оси 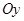 , имеющих положительные ординаты и обладающие тем свойством, что касательные, проведенные через каждую из таких точек к графику функции
, имеющих положительные ординаты и обладающие тем свойством, что касательные, проведенные через каждую из таких точек к графику функции 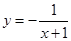 , высекают на оси абсцисс отрезок длины
, высекают на оси абсцисс отрезок длины 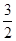 .
.
36) В декартовой прямоугольной системе координат на плоскости заданы две параболы:  . Найдите минимальное значение расстояния между двумя точками, одна из которых принадлежит первой параболе, а другая – второй параболе.
. Найдите минимальное значение расстояния между двумя точками, одна из которых принадлежит первой параболе, а другая – второй параболе.
37)  При каких значениях
При каких значениях  кривые
кривые  и
и 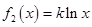 имеют одну общую точку?
имеют одну общую точку?
38) Найдите геометрическое место точек – вершин парабол 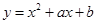 , каждая из которых касается прямой
, каждая из которых касается прямой 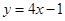 .
.
Ответы.
1) а) Касательная 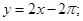 нормаль
нормаль  .
.
б) Касательная  нормаль
нормаль  .
.
в) Касательная  нормаль
нормаль 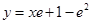 .
.
г) Касательная  нормаль
нормаль  .
.
д) Касательная 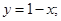 нормаль
нормаль 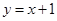 .
.
2)  . 3)
. 3)  . 4)
. 4)  .
.
5) а)  ; б)
; б)  . 6)
. 6)  .
.
7) 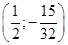 . 9)
. 9) 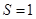 . 11)
. 11)  . 12)
. 12) 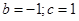 .
.
13)  . 14)
. 14)  . 15)
. 15) 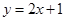 . 16)
. 16) 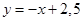 .
.
17)  . 18)
. 18)  . 19)
. 19) 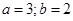 . 20)
. 20) 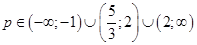 . 21) а)
. 21) а)  . б)
. б) 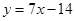 . 22)
. 22)  .
.
23) 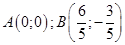 . 24)
. 24)  . 25)
. 25)  .
.
26) а)  . б)
. б)  . 27)
. 27)  . 28)
. 28)  .
.
30) Общие точки 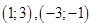 являются точками касания. 31)
являются точками касания. 31)  .
.
32)  . 33) Да.
. 33) Да. 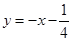 . 34)
. 34)  . 35)
. 35) 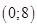 .
.
36)  . 37)
. 37)  . 38) Прямая
. 38) Прямая  .
.
Дата добавления: 2015-07-20; просмотров: 1238 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрический смысл производной. Касательная. | | | SCREAM SCHOOL 1 страница |