Читайте также:
|
Систему уравнений записать в матричной форме и решить: а) с помощью обратной матрицы, б) с помощью правила Крамера и в) методом Гаусса.
1 вариант. 
2 вариант. 
3 вариант.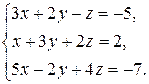 
4 вариант. 
5 вариант. 
6 вариант. 
7 вариант. 
8 вариант.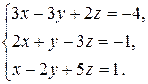 
9 вариант. 
10 вариант.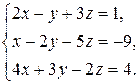 
11 вариант. 
12 вариант. 
13 вариант. 
14 вариант. 
15 вариант. 
16 вариант. 
17 вариант. 
18 вариант.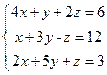 
19 вариант.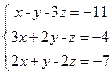 
20 вариант. 
Образец решения типового варианта
Задача 1. Написать разложение вектора 
по векторам 
Решение.
Задача 2. Коллинеарны ли векторы 
и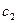 
, построенные по векторам 
и 
?
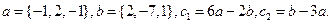
Решение.
Вычисляем координаты векторов
Они пропорциональны
векторы и 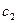коллинеарны.
Задача 3. Найти косинус угла между векторами 
и 
.
Решение.
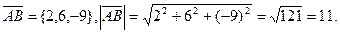
Задача 4. Вычислить площадь параллелограмма, построенного на векторах и .
Решение.
S=31 кв.ед.
Задача 5. Компланарны ли векторы , и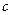 
.
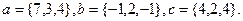
Решение.
Составляем определитель из координат векторов. Если он равен нулю, векторы компланарны.
векторы , и 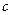не компланарны.
Задача 6. Вычислить объем тетраэдра с вершинами в точках 
и его высоту, опущенную из вершины 
на грань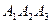 
.
Решение.
Задача 7. Найти расстояние от точки 
до плоскости, проходящей через точки 
.
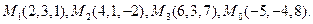
Решение.
Уравнение плоскости, проходящей через 3 точки
d =11.
Задача 8. Написать уравнение плоскости, проходящей через точку 
перпендикулярно вектору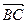 
.
Решение.
Находим 
Т.к. вектор 
искомой плоскости, то его можно взять в качестве вектора нормали, следовательно
Ответ: 3x-y-z+6=0.
Задача 9. Найти угол между плоскостями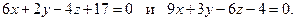 
Решение.
Находим векторы, угол между которыми соответствует искомому углу между плоскостями.
То есть плоскости параллельны.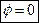 
Задача 12. Написать канонические уравнения прямой.
Решение.
Направляющий вектор прямой найдем так
Найдем координаты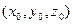 
одной из точек, через которые проходит искомая прямая. Для этого дадим координате 
произвольное значение, например,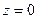 
, которое подставим в уравнения заданных плоскостей.
Итак, получается точка с координатами 
Тогда уравнение прямой имеет вид
Задача 13. Найти точку пересечения прямой и плоскости.
Подставим в уравнение плоскости
Полученное значение подставим в систему
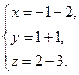
Таким образом, координаты искомой точки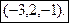 
Задача 14. Вычислить сумму матриц kA+mB,
если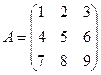 
, 
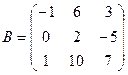k=2, m=-3
Решение:
Элементы матрицы суммы определяются по формуле:
Сij=kaij+mbij.
Вычислим элементы первой строки матрицы суммы:
С11=2·1+(-3) ·(-1)=5; С12=2·2+(-3) ·6=-14; С13=2·3+(-3) ·(-3)=15.
Аналогично вычисляем остальные элементы:
С21=2·4+(-3) ·0=8; С22=2·5+(-3) ·2=4; С23=2·6+(-3) ·(-5)=27.
С31=2·7+(-3) ·1=11; С32=2·8+(-3) ·10=-14; С33=2·9+(-3) ·7=-9.
Таким образом, матрица суммы примет вид:
Задача 15,a. Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы
.
Решение.
Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).
Вычислим определитель данной системы:
,
следовательно, система имеет единственное решение.
Данную систему можно записать в матричной форме:
, где 
, 
, 
.
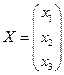Так как 
, то для матрицы 
существует обратная матрица 
. Умножив матричное уравнение слева на , получим 
, откуда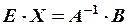 
, или 
.
Найдем обратную матрицу по формуле
,
где 
алгебраическое дополнение элемента 
.
,
,
.
.
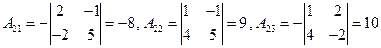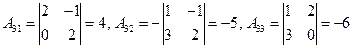Тогда 
.
Ответ: 
.
Дата добавления: 2015-07-25; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 8. | | | Решение системы находим по формулам Крамера |