
Читайте также:
|
Линии, определяемые уравнениями второй степени с двумя текущими координатами

называются кривыми второго порядка. Это уравнение на плоскости (если не считать случаев вырождения и распадения) определяет окружность, эллипс, гиперболу, параболу.
Окружность – множество точек плоскости_ _ _ _ _ _ _
Расстояние от точки окружности до центра называется _ _ _ _ _ _ _
Уравнение окружности радиуса  с центром в точке
с центром в точке 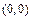 имеет вид
имеет вид

уравнение окружности радиуса  с центром в точке
с центром в точке  :
:
 .
.
Эллипс – множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Обозначим фокусы через 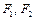 , расстояние между ними через , расстояние между ними через  , сумму расстояний от произвольной точки эллипса до фокусов через , сумму расстояний от произвольной точки эллипса до фокусов через  . По определению _ _ _ _ _ _ _Выберем ДСК так, чтобы фокусы лежали на оси . По определению _ _ _ _ _ _ _Выберем ДСК так, чтобы фокусы лежали на оси 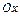 , а начало координат совпадало с серединой отрезка , а начало координат совпадало с серединой отрезка  . Тогда фокусы будут иметь координаты_ _ _ _ _ _ _
Пусть . Тогда фокусы будут иметь координаты_ _ _ _ _ _ _
Пусть  – произвольная точка эллипса. По определению имеем – произвольная точка эллипса. По определению имеем  , т.е. , т.е.
|
Обозначим  . Тогда получим
. Тогда получим

– каноническое уравнение эллипса.
Числа  называются полуосями эллипса. Степень «вытянутости» эллипса характеризует эксцентриситет
называются полуосями эллипса. Степень «вытянутости» эллипса характеризует эксцентриситет
 .
.
 Привести к каноническому виду уравнение
Привести к каноническому виду уравнение  и построить кривую.
и построить кривую.
Гипербола – множество точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы через 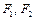 , расстояние между ними через , расстояние между ними через  , модуль разности расстояний от произвольной точки гиперболы до фокусов через , модуль разности расстояний от произвольной точки гиперболы до фокусов через  . По определению_ _ _ _ _ _ Выберем ДСК так, чтобы фокусы лежали на оси . По определению_ _ _ _ _ _ Выберем ДСК так, чтобы фокусы лежали на оси 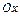 , а начало координат совпадало с серединой отрезка , а начало координат совпадало с серединой отрезка  .
Доказать САМОСТОЯТЕЛЬНО, что уравнение гиперболы в этом случае имеет вид .
Доказать САМОСТОЯТЕЛЬНО, что уравнение гиперболы в этом случае имеет вид
|
 ,
,
где обозначено  .
.
Здесь Числа  – действительная,
– действительная,  – мнимая полуоси гиперболы, прямые
– мнимая полуоси гиперболы, прямые  называются асимптотами.
называются асимптотами.
Эксцентриситет гиперболы  .
.
 Привести к каноническому виду уравнение
Привести к каноническому виду уравнение  , построить кривую, найти координаты фокусов.
, построить кривую, найти координаты фокусов.
Парабола – множество точек плоскости, каждая из которых одинаково удалена от данной точки  , называемой фокусом, и данной прямой
, называемой фокусом, и данной прямой  , называемой директрисой. Расстояние
, называемой директрисой. Расстояние 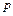 от фокуса до директрисы называется параметром параболы.
от фокуса до директрисы называется параметром параболы.
Выберем ДСК как указано на рисунке. Тогда
 Построить параболу
Построить параболу  .
.
Дата добавления: 2015-07-11; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Грамотность построения сайта | | | ЗАДАНИЕ №3 Решить следующие задачи |