
|
Читайте также: |
Таким образом, независимо от типа рассеивающего объекта и способа его освещения вероятность одновременного равенства нулю всех компонент поля в произвольной точке пространства стремится к нулю. Поэтому точку нуля амплитуды и соответственно линию нуля как функцию трех координат в пространстве можно вводить только для отдельно взятой компоненты поля.
Отметим, что гипотетично можно предположить вариант поля сразу за объектом, при котором коэффициенты в выражении (3.7) для 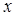 - и
- и 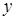 -компонент не являются независимыми (например, освещение объекта первого типа циркулярно поляризованным светом). В такой ситуации, в некоторой точке пространства нуль амплитуды для
-компонент не являются независимыми (например, освещение объекта первого типа циркулярно поляризованным светом). В такой ситуации, в некоторой точке пространства нуль амплитуды для 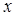 - и
- и 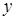 -компонентполя будет достигаться одновременно и суммарное поле в окрестности такой точки будет определяться только
-компонентполя будет достигаться одновременно и суммарное поле в окрестности такой точки будет определяться только  -компонентой поля. Однако в любом случае можно утверждать, что в статистических когерентных полях абсолютный нуль амплитуды поля не достигается.
-компонентой поля. Однако в любом случае можно утверждать, что в статистических когерентных полях абсолютный нуль амплитуды поля не достигается.
Рассмотрим более подробно поле вблизи точки «нуля» амплитуды, возникающего в рамках скалярного приближения для однородно поляризованной волны. Как показано в [5; 7; 8], при приближении к точке нуля амплитуды модуль градиента фазы поля неограниченно возрастает, что в свою очередь приводит к резкому изменению направления волнового вектора и полной его неопределенности в точке нуля амплитуды. Однако волновой вектор определяется всеми тремя компонентами поля и соответственно его ориентация и величина определяется  -компонентой поля. Более того, при приближении к «нулю» амплитуды, определяющая роль ненулевых компонент увеличивается независимо от соотношения между средними модулями амплитуд
-компонентой поля. Более того, при приближении к «нулю» амплитуды, определяющая роль ненулевых компонент увеличивается независимо от соотношения между средними модулями амплитуд  ,
,  ,
,  . Поскольку пространственный масштаб модуляции поля для различных компонент соизмеримый, то можно утверждать, что скорость изменения волнового вектора (его ориентации) в точке «нуля» амплитуды соизмерима со скоростью изменения волнового вектора в любой другой точке поля.
. Поскольку пространственный масштаб модуляции поля для различных компонент соизмеримый, то можно утверждать, что скорость изменения волнового вектора (его ориентации) в точке «нуля» амплитуды соизмерима со скоростью изменения волнового вектора в любой другой точке поля.
3.1.2. «Абсолютный» нуль интенсивности как модель оптической сингулярности
Очевидно, что при рассмотрении физических ситуаций, которые можно считать адекватными проявлениям абсолютного нуля амплитуды поля, к ним можно подходить, исходя из следующих, в некоторой мере, тривиальных соображений: физическая ситуация будет восприниматься исследователем как ситуация, адекватная абсолютному нулю амплитуды, если используемые им методы исследования поля не дают возможности отличить реальную ситуацию от поведения поля в окрестности абсолютного нуля амплитуды.
Естественно, что такое утверждение является справедливым и для других нереализуемых оптических сингулярностей, например, краевой дислокации скалярного поля или вихря с топологическим зарядом по модулю большим чем единица и т.д.
Для физической ситуации, адекватной наличию в поле абсолютного нуля амплитуды, сформулированное утверждение может быть уточнено:
1. Очевидно, что для объектов второго типа, преобразующих поляризацию облучающего пучка (по крайней мере,  и
и  соизмеримы между собой), такая физическая ситуация возникает, когда в некоторой точке наблюдения трехмерные линии нулей всех трех компонент поля сближаются на расстояние соизмеримое с пространственной разрешающей способностью измерительного прибора, с помощью которого анализируется поле. Очевидно, что предельная величина, на которую могут сойтись нулевые линии, и при этом позиции нулей компонент могут быть идентифицированы как различные, сравнима с длиной волны излучения. В такой ситуации никакими оптическими способами, использующими ту же длину волны, невозможно отличить образовавшуюся полевую структуру от структуры, возникающей в области «абсолютного» нуля. Вероятность сближения всех трех линий нулей на расстояние, соизмеримое с разрешающей способностью (длиной волны) является конечной величиной и может быть оценена с помощью результатов, полученных в [8].
соизмеримы между собой), такая физическая ситуация возникает, когда в некоторой точке наблюдения трехмерные линии нулей всех трех компонент поля сближаются на расстояние соизмеримое с пространственной разрешающей способностью измерительного прибора, с помощью которого анализируется поле. Очевидно, что предельная величина, на которую могут сойтись нулевые линии, и при этом позиции нулей компонент могут быть идентифицированы как различные, сравнима с длиной волны излучения. В такой ситуации никакими оптическими способами, использующими ту же длину волны, невозможно отличить образовавшуюся полевую структуру от структуры, возникающей в области «абсолютного» нуля. Вероятность сближения всех трех линий нулей на расстояние, соизмеримое с разрешающей способностью (длиной волны) является конечной величиной и может быть оценена с помощью результатов, полученных в [8].
Естественно, что, учитывая статистическую независимость компонент поля, стабильность таких образований во френелевской зоне невелика. Поэтому «абсолютний» нуль в этой области распространения волны является «точечным» дефектом. При этом, чем ближе к зоне Фурье, тем больше продольные размеры такого образования, и на достаточно большом расстоянии от объекта, в зоне, где распространение поля сводится практически к его масштабному преобразованию, можно говорить о возможности существования «линий абсолютного» нуля векторного поля. Однако необходимо отметить, что вероятность образования такой структуры достаточно мала, а их количество несоизмеримо меньше, чем количество нулевых линий, отождествляемых с компонентами поля.
2. Несколько иная ситуация складывается для рассеивающих объектов, не преобразующих поляризацию облучающего пучка.
Пусть в некоторой точке основная компонента (или компоненты, если поляризация облучающего пучка эллиптическая) поля достигает нуля. Суммарное поле в окрестности такой точки определяется ненулевыми компонентами. При соответствующих соотношениях между  ,
,  ,
,  и расстоянии
и расстоянии  до зоны наблюдения поперечные размеры такой окрестности соизмеримы с пространственной разрешающей способностью измерительного прибора (длиной волны излучения). При этом с возрастанием
до зоны наблюдения поперечные размеры такой окрестности соизмеримы с пространственной разрешающей способностью измерительного прибора (длиной волны излучения). При этом с возрастанием  размеры окрестности уменьшаются, поскольку отношение средних интенсивностей основной и неосновной компоненты (компонент) постоянно уменьшается. В предельном случае (размеры области «абсолютного» нуля сравнимы с длиной волны излучения) можно утверждать, что в этой окрестности никакими оптическими способами, использующими ту же длину волны, невозможно определить поле, соответствующее неосновным компонентам.
размеры окрестности уменьшаются, поскольку отношение средних интенсивностей основной и неосновной компоненты (компонент) постоянно уменьшается. В предельном случае (размеры области «абсолютного» нуля сравнимы с длиной волны излучения) можно утверждать, что в этой окрестности никакими оптическими способами, использующими ту же длину волны, невозможно определить поле, соответствующее неосновным компонентам.
В рамках этих соображений можно утверждать, что, начиная с некоторого расстояния  , в пространстве существуют лини абсолютного нуля, соответствующие линиям нуля основной компоненты поля.
, в пространстве существуют лини абсолютного нуля, соответствующие линиям нуля основной компоненты поля.
3.1.3. Поляризационная модуляция поля в окрестности «абсолютного» нуля амплитуд
Рассмотрим поведение характеристик поля в области, в которой реализуется модель абсолютного нуля векторного поля.
Перейдем к локальной системе координат, в которой ось  направлена вдоль нормали к результирующему волновому фронту. В такой системе координат присутствуют только две компоненты амплитуды поля. Начало локальной системы координат разместим в точке нуля амплитуд, плоскость
направлена вдоль нормали к результирующему волновому фронту. В такой системе координат присутствуют только две компоненты амплитуды поля. Начало локальной системы координат разместим в точке нуля амплитуд, плоскость  совпадает с плоскостью колебания результирующего вектора напряженности электрического поля (см. рис. 3.1.). Такое преобразование может быть осуществлено простым поворотом локальной системы координат
совпадает с плоскостью колебания результирующего вектора напряженности электрического поля (см. рис. 3.1.). Такое преобразование может быть осуществлено простым поворотом локальной системы координат 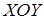 . В системе координат
. В системе координат  компонента поля
компонента поля 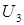 равна нулю. Можно показать, что и в этой системе координат поле в малой окрестности произвольной точки также описывается соотношениями типа (3.7). Коэффициенты при
равна нулю. Можно показать, что и в этой системе координат поле в малой окрестности произвольной точки также описывается соотношениями типа (3.7). Коэффициенты при 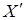 ,
,  и нулевые члены также статистически независимые величины. Для простоты будем обозначать их теми же индексами.
и нулевые члены также статистически независимые величины. Для простоты будем обозначать их теми же индексами.
Тангенс фазы компоненты  в окрестности нуля амплитуды запишется в виде
в окрестности нуля амплитуды запишется в виде
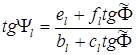 . (3.11)
. (3.11)
Выражение (3.11) – тангенс фазы вихря компоненты в зоне ядра вихря.
Для простоты предположим, что в зоне ядра вихри компонент – изотропные вихри. Можно показать, что в случае анизотропных вихрей общие закономерности поляризационной модуляции существенно не зависят от отличия фронта таких вихрей от «идеального» геликоида.

 1. Предположим, что знаки вихрей, ассоциируемых с
1. Предположим, что знаки вихрей, ассоциируемых с 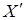 - и
- и  -компонентами поля одинаковые. Тогда разность фаз между компонентами равна
-компонентами поля одинаковые. Тогда разность фаз между компонентами равна  для каждой точки окрестности. Это означает, что в окрестности нуля поле поляризационно-однородное. Поляризация в общем случае эллиптическая. Эксцентриситет эллипса зависит как от разности фаз, так и от соотношения модулей амплитуд компонент
для каждой точки окрестности. Это означает, что в окрестности нуля поле поляризационно-однородное. Поляризация в общем случае эллиптическая. Эксцентриситет эллипса зависит как от разности фаз, так и от соотношения модулей амплитуд компонент  и
и 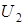 . Характерное поведение поля в окрестности нуля иллюстрируется рис. 3.2 а.
. Характерное поведение поля в окрестности нуля иллюстрируется рис. 3.2 а.
2. Знаки компонентных вихрей разные. Разность фаз между компонентами соответственно равняется, с точностью до знака, 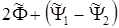 . Поведение поля в окрестности нуля в этой ситуации иллюстрируется рис. 3.2 b (для определенности
. Поведение поля в окрестности нуля в этой ситуации иллюстрируется рис. 3.2 b (для определенности  ). Вдоль линий, выходящих из точки нуля под углами
). Вдоль линий, выходящих из точки нуля под углами  и
и  , поляризация линейная. Вдоль линий под углами
, поляризация линейная. Вдоль линий под углами  и
и 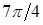 – поле поляризовано циркулярно. В промежутках между этими значениями поле поляризовано эллиптически.
– поле поляризовано циркулярно. В промежутках между этими значениями поле поляризовано эллиптически.
Можно показать, что в случае, если геликоидальный фронт отличается от идеального, будет наблюдаться определенное изменение эксцентриситетов эллипсов, пространственное смещение характерных направлений (вдоль которых поляризация линейна или циркулярна). Однако общие тенденции поведения поля в окрестности нуля амплитуд остаются без изменений.
Поскольку в этом параграфе мы рассматриваем поведение поля в окрестности модельных сингулярностей, то проанализируем также ситуацию, когда в компонентах поля реализуются краевые дислокации.
В этом случае  и возможны три следующих реализаций параметров поля:
и возможны три следующих реализаций параметров поля:
а) 
 при
при 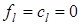 ;
;
b)  при
при  ;
;
c)  при
при 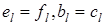 , или
, или  .
.
Детальные иллюстрации поведения поля в случае компонентных краевых дислокаций приводить не будем, рассмотрим лишь случай, когда в компонентах 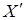 и
и  краевые дислокации направлены перпендикулярно одна к другой. Тогда поле компонент описывается соотношениями:
краевые дислокации направлены перпендикулярно одна к другой. Тогда поле компонент описывается соотношениями:
 . (3.12)
. (3.12)
В общем случае поле при обходе точки нуля также эллиптически поляризовано. Вместе с тем, эксцентриситет эллипсов меняется в соответствии со значением  . Характерный тип поведения поля иллюстрируется рис. 3.3 a. Для того, чтобы подчеркнуть, что при обходе точки нуля на
. Характерный тип поведения поля иллюстрируется рис. 3.3 a. Для того, чтобы подчеркнуть, что при обходе точки нуля на  фаза излучения изменяется на противоположную, тут и далее для линейной поляризации указано только одно направление колебания вектора поля. Различное направление стрелочек коллинеарных векторов соответствует тому, что поля в этих точках находятся в противофазе. Интересным является случай, когда
фаза излучения изменяется на противоположную, тут и далее для линейной поляризации указано только одно направление колебания вектора поля. Различное направление стрелочек коллинеарных векторов соответствует тому, что поля в этих точках находятся в противофазе. Интересным является случай, когда  . Тут поляризация в окрестности точки нуля линейная, а вектор поля осуществляет поворот на
. Тут поляризация в окрестности точки нуля линейная, а вектор поля осуществляет поворот на 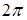 при обходе точки нуля (рис. 3.3 b).
при обходе точки нуля (рис. 3.3 b).
В заключение отметим, что представленный набор поляризационных ситуаций в окрестности абсолютного нуля поля далеко не исчерпан. Возможны комбинации краевой и винтовой дислокаций, разнообразные реализации краевых дислокаций и т.д.
3.2. Дисклинации. Поляризационные сингулярности
Отметим, что в силу векторной природы электромагнитного поля, необходимо четко различать поле общего вида и поле, которое может быть описано с помощью параксиального приближения. Как показано в [3; 64 – 66; 73], системы сингулярностей для этих случаев различны.
 Поэтому в дальнейшем будем считать, что рассматриваемые нами поля подчиняются параксиальному приближению. Для такого типа полей можно выделить временные нулевые сингулярности – дисклинации, множества точек в которых компоненты поля принимают нулевое значение в определенный момент времени [3; 65]. Существование подобных структур легко представить, обратившись к рисунку 3.4.
Поэтому в дальнейшем будем считать, что рассматриваемые нами поля подчиняются параксиальному приближению. Для такого типа полей можно выделить временные нулевые сингулярности – дисклинации, множества точек в которых компоненты поля принимают нулевое значение в определенный момент времени [3; 65]. Существование подобных структур легко представить, обратившись к рисунку 3.4.
 Предположим, что преимущественное направление распространения поля совпадает с осью
Предположим, что преимущественное направление распространения поля совпадает с осью  и в силу параксиального приближения
и в силу параксиального приближения  -компонентой поля можно пренебречь. Пусть в некоторой точке
-компонентой поля можно пренебречь. Пусть в некоторой точке  поле поляризовано линейно. Разложим поле
поле поляризовано линейно. Разложим поле  на ортогональные линейно поляризованные компоненты
на ортогональные линейно поляризованные компоненты  в соответствии с базисом, изображенным на рисунке. Как следует из рисунка,
в соответствии с базисом, изображенным на рисунке. Как следует из рисунка,  -компонента тождественно равна нулю. Иными словами, для компоненты
-компонента тождественно равна нулю. Иными словами, для компоненты 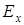 в точке
в точке  наблюдается вихрь. В то же время компонента
наблюдается вихрь. В то же время компонента 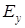 дважды за период колебания обращается в нуль. Таким образом, именно в эти моменты времени суммарная амплитуда поля равна нулю, т.е. в точке
дважды за период колебания обращается в нуль. Таким образом, именно в эти моменты времени суммарная амплитуда поля равна нулю, т.е. в точке  наблюдается дисклинация.
наблюдается дисклинация.

 Заметим, что в точке с эллиптической поляризацией поле никогда не принимает нулевого значения. Отсюда можно сделать вывод, что место жизни дисклинаций – точки поля, где оно поляризовано линейно. Достаточно просто показать, что в силу непрерывности поля такие точки образуют в плоскости замкнутые односвязные линии (в трехмерном пространстве поверхности), отделяющие области с разным направлением поляризации (см. рис. 3.5). Эти линии будем называть
Заметим, что в точке с эллиптической поляризацией поле никогда не принимает нулевого значения. Отсюда можно сделать вывод, что место жизни дисклинаций – точки поля, где оно поляризовано линейно. Достаточно просто показать, что в силу непрерывности поля такие точки образуют в плоскости замкнутые односвязные линии (в трехмерном пространстве поверхности), отделяющие области с разным направлением поляризации (см. рис. 3.5). Эти линии будем называть  -контурами (в пространстве
-контурами (в пространстве 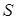 -поверхностями) [3].
-поверхностями) [3].
Возможность существования дисклинации на  -контуре не налагает никаких ограничений на азимут поляризации в каждой его точке. Более того можно утверждать, что азимут линейной поляризации непрерывно меняется вдоль
-контуре не налагает никаких ограничений на азимут поляризации в каждой его точке. Более того можно утверждать, что азимут линейной поляризации непрерывно меняется вдоль  -контура, поскольку в противном случае пришлось бы допустить возможность существования для одной из поляризационных проекций поля краевой дислокации – поверхности, в каждой точке которой поле проекции равно нулю. Однако, как было показано в п. 2.3, существование таких дефектов поля невозможно.
-контура, поскольку в противном случае пришлось бы допустить возможность существования для одной из поляризационных проекций поля краевой дислокации – поверхности, в каждой точке которой поле проекции равно нулю. Однако, как было показано в п. 2.3, существование таких дефектов поля невозможно.
Длина  -контуров в общем случае может меняться от нуля (вырожденный случай, когда
-контуров в общем случае может меняться от нуля (вырожденный случай, когда  -контур преобразуется в точку) до бесконечности, а средняя длина
-контур преобразуется в точку) до бесконечности, а средняя длина  -контура зависит (как будет показано далее) от преимущественной поляризации векторного поля. В частности, для абсолютно случайного поля (глобально деполяризованного c Гауссово-распределенными характеристиками [74 – 76]) возможна лишь структура
-контура зависит (как будет показано далее) от преимущественной поляризации векторного поля. В частности, для абсолютно случайного поля (глобально деполяризованного c Гауссово-распределенными характеристиками [74 – 76]) возможна лишь структура  -контуров (рис. 3.5 а), когда область с определенным направлением поляризации (или несколько таких областей) вкладывается в область с другой поляризацией, в свою очередь ограниченную областью, в которой направление вращения вектора напряженности поля снова меняет свое направление на противоположный и т.д. Образно говоря, для такого поля реализуется структура
-контуров (рис. 3.5 а), когда область с определенным направлением поляризации (или несколько таких областей) вкладывается в область с другой поляризацией, в свою очередь ограниченную областью, в которой направление вращения вектора напряженности поля снова меняет свое направление на противоположный и т.д. Образно говоря, для такого поля реализуется структура  -контуров типа «матрешка». При этом максимальный размер самой «большой» из них не ограничен. Другой возможный тип структуры
-контуров типа «матрешка». При этом максимальный размер самой «большой» из них не ограничен. Другой возможный тип структуры  -контуров («острова в океане») в таком поле не реализуется, поскольку в этом случае, даже при равенстве площадей, которые будут занимать области с разным направлением поляризации, право- и левополяризованные состояния поля не будут равноправны.
-контуров («острова в океане») в таком поле не реализуется, поскольку в этом случае, даже при равенстве площадей, которые будут занимать области с разным направлением поляризации, право- и левополяризованные состояния поля не будут равноправны.
 Таким образом,
Таким образом,  -контура как место жизни дисклинаций представляют собой особую структуру векторного поля. С другой стороны, понятие дисклинации как дефекта поля является фундаментальным только для электромагнитных волн радиодиапазона. Для оптики эти дефекты поля «не существуют» из-за быстрых изменений поля и невозможности прямого измерения амплитуды колебания.
-контура как место жизни дисклинаций представляют собой особую структуру векторного поля. С другой стороны, понятие дисклинации как дефекта поля является фундаментальным только для электромагнитных волн радиодиапазона. Для оптики эти дефекты поля «не существуют» из-за быстрых изменений поля и невозможности прямого измерения амплитуды колебания.
 В оптическом смысле, более интересными являются стационарные или «поляризационные» сингулярности векторного поля. Действительно, в каждой точке пространства конец электрического вектора описывает поляризационные эллипсы, параметры которых (азимут поляризации, направление вращения вектора поля
В оптическом смысле, более интересными являются стационарные или «поляризационные» сингулярности векторного поля. Действительно, в каждой точке пространства конец электрического вектора описывает поляризационные эллипсы, параметры которых (азимут поляризации, направление вращения вектора поля  ) как функция пространственных координат тоже могут иметь сингулярности.
) как функция пространственных координат тоже могут иметь сингулярности.
Для параксиального приближения вводится два основных типа таких сингулярностей [3; 64 – 67; 73; 77 – 86]:
1. К первым относят уже знакомые  -контура (в пространстве
-контура (в пространстве  -поверхности), поскольку направление вращения вектора электрического поля вдоль них неопределенно. Связь
-поверхности), поскольку направление вращения вектора электрического поля вдоль них неопределенно. Связь  -контуров с дисклинациями естественна и есть проявлением того, что все особые множества одной физической величины (например, для скалярного поля фаза и интенсивность, см. п. 2.6) связны между собой.
-контуров с дисклинациями естественна и есть проявлением того, что все особые множества одной физической величины (например, для скалярного поля фаза и интенсивность, см. п. 2.6) связны между собой.
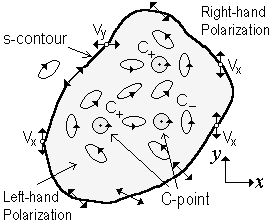
2.  -точки (в пространстве
-точки (в пространстве  -линии) – точки циркулярной поляризации поля (см. рис. 3.6), в которых поляризационный эллипс вырождается в круг и, соответственно, неопределенным является направление главной оси (азимут) поляризационного эллипса и как следствие значение главной фазы [80], определяющей положение электрического вектора относительно большой оси эллипса [3; 73]. Естественно, что
-линии) – точки циркулярной поляризации поля (см. рис. 3.6), в которых поляризационный эллипс вырождается в круг и, соответственно, неопределенным является направление главной оси (азимут) поляризационного эллипса и как следствие значение главной фазы [80], определяющей положение электрического вектора относительно большой оси эллипса [3; 73]. Естественно, что  -точку как топологический элемент можно характеризовать двояко:
-точку как топологический элемент можно характеризовать двояко:
· топологическим зарядом сингулярности главной фазы (vibration phase):
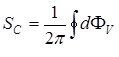 (3.1)
(3.1)
· и топологическим зарядом сингулярности азимута
 , (3.2)
, (3.2)
который совпадает с индексом Пуанкаре  -точки. В дальнейшем будем называть
-точки. В дальнейшем будем называть  просто зарядом
просто зарядом  -точки, а
-точки, а  просто ее индексом.
просто ее индексом.

 Покажем, что, в отличие от зарядов и индексов скалярных особых точек, эти величины принимают значения, кратные
Покажем, что, в отличие от зарядов и индексов скалярных особых точек, эти величины принимают значения, кратные  . В частности, при обходе С -точки по замкнутому контуру азимут поляризации осуществляет поворот на угол, равный по модулю
. В частности, при обходе С -точки по замкнутому контуру азимут поляризации осуществляет поворот на угол, равный по модулю  [83; 84]. Заметим, что существование
[83; 84]. Заметим, что существование  -точек, при обходе которых оси эллипсов осуществляют большее количество оборотов, не запрещено, однако такие полевые структуры являются топологически и физически неустойчивыми. Поэтому будем считать, что индекс и заряд
-точек, при обходе которых оси эллипсов осуществляют большее количество оборотов, не запрещено, однако такие полевые структуры являются топологически и физически неустойчивыми. Поэтому будем считать, что индекс и заряд  -точки могут принимать значения только
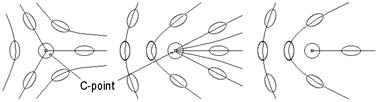
-точки могут принимать значения только  . В [3; 66] показано, что только три типа поведения эллипсов вокруг
. В [3; 66] показано, что только три типа поведения эллипсов вокруг  -точки возможно (см. рис. 3.7). Эти пространственные распределения эллипсов получили названия: “star”, “monstar” и “lemon” соответственно.
-точки возможно (см. рис. 3.7). Эти пространственные распределения эллипсов получили названия: “star”, “monstar” и “lemon” соответственно.
Установим взаимосвязь между величиной  и значением
и значением 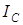 . Такое рассмотрение достаточно просто провести, если использовать разложение поля на ортогональные циркулярно поляризованные компоненты. Заметим, что координаты
. Такое рассмотрение достаточно просто провести, если использовать разложение поля на ортогональные циркулярно поляризованные компоненты. Заметим, что координаты  -точки, находящейся в области с определенным направлением поляризации (левым или правым), совпадают с координатами вихря ортогонально поляризованной компоненты. Именно в центре вихря ее модуль амплитуды равен нулю и суммарное поле строго циркулярно поляризовано.
-точки, находящейся в области с определенным направлением поляризации (левым или правым), совпадают с координатами вихря ортогонально поляризованной компоненты. Именно в центре вихря ее модуль амплитуды равен нулю и суммарное поле строго циркулярно поляризовано.
Для фаз лево- и право циркулярно поляризованных компонент выполняются такие соотношения [3; 81]:
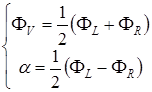 , (3.3)
, (3.3)
где  – главная фаза колебания (vibration phase);
– главная фаза колебания (vibration phase);  – фазы право- и лево циркулярной компонент соответственно.
– фазы право- и лево циркулярной компонент соответственно.
Предположим, что в некоторой области поля (для определенности области с правой поляризацией) наблюдается  -точка. Тогда координаты этой точки совпадают с вихрем левополяризованной компоненты. Исходя из этого, правополяризованная компонента «гладкая» в области анализа, а ортогональная ей компонента содержит сингулярность фазы в
-точка. Тогда координаты этой точки совпадают с вихрем левополяризованной компоненты. Исходя из этого, правополяризованная компонента «гладкая» в области анализа, а ортогональная ей компонента содержит сингулярность фазы в  -точке. Тогда имеет место система [3]
-точке. Тогда имеет место система [3]
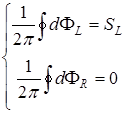 , (3.4)
, (3.4)
где  – топологический заряд вихря левой компоненты.
– топологический заряд вихря левой компоненты.
Поскольку  , то из (3.2) и (3.3) следует, что:
, то из (3.2) и (3.3) следует, что:
 . (3.5)
. (3.5)
Учитывая, что заряд вихря  , получаем:
, получаем:
 . (3.6)
. (3.6)
Если  -точка находится в области с левой поляризацией, имеет место система, аналогичная (3.5):
-точка находится в области с левой поляризацией, имеет место система, аналогичная (3.5):
 (3.7)
(3.7)
или для области с левой поляризацией
 . (3.8)
. (3.8)
Соотношения (3.6) и (3.8) можно объединить в одно, если ввести так называемый handedness фактор 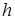 , равный
, равный 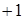 для области с правой поляризацией, и
для области с правой поляризацией, и  для регионов поля с левой поляризацией.
для регионов поля с левой поляризацией.
С учетом 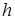 (3.6) и (3.8) перепишется
(3.6) и (3.8) перепишется
 . (3.9)
. (3.9)
Такая взаимосвязь между зарядом и индексом отражает закономерности изменений поля в области  - точки не только пространственные (ориентацию эллипсов), но и временные. Например, мгновенная ориентация вектора поля в области с левой (рис. 3.8 a) или правой (рис. 3.8 b) поляризацией может быть реализована только при определенном распределении азимута и главной фазы в области. Разрешенные поведения поля в окрестности
- точки не только пространственные (ориентацию эллипсов), но и временные. Например, мгновенная ориентация вектора поля в области с левой (рис. 3.8 a) или правой (рис. 3.8 b) поляризацией может быть реализована только при определенном распределении азимута и главной фазы в области. Разрешенные поведения поля в окрестности  -точки иллюстрируются рисунками 3.8 a и 3.8 b и запрещенные рисунком 3.8 c. При поведении поля, подобном изображенному на рис. 3.8 c при пересечении
-точки иллюстрируются рисунками 3.8 a и 3.8 b и запрещенные рисунком 3.8 c. При поведении поля, подобном изображенному на рис. 3.8 c при пересечении  -точки возникает разрыв (скачок характеристик) поля. Другими словами, увеличение (уменьшение) главной фазы при обходе
-точки возникает разрыв (скачок характеристик) поля. Другими словами, увеличение (уменьшение) главной фазы при обходе  -сингулярности обеспечивает «компенсацию» дополнительного поворота вектора поля, возникающего из-за вращения осей эллипсов в окрестности
-сингулярности обеспечивает «компенсацию» дополнительного поворота вектора поля, возникающего из-за вращения осей эллипсов в окрестности  -точки.
-точки.
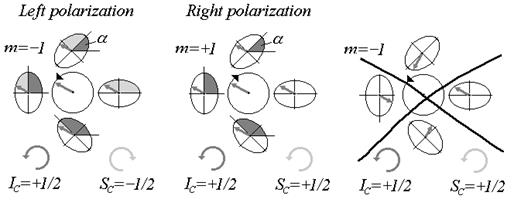
a) b) c)
Рис. 3.8
Иллюстрация временного поведения вектора поля в окрестности  -точки.
-точки.
Изменение площади темных серых областей на рисунках (a) и (b) иллюстрирует поведение азимута поляризации вокруг  -точки. Величина светло-серых областей на рисунке (a) указывает, каким образом меняется главная фаза в окрестности
-точки. Величина светло-серых областей на рисунке (a) указывает, каким образом меняется главная фаза в окрестности  -сингулярности. Темно-серые и светло-серые круговые стрелки в нижней части каждого рисунка указывают направление увеличения главной фазы (знак заряда
-сингулярности. Темно-серые и светло-серые круговые стрелки в нижней части каждого рисунка указывают направление увеличения главной фазы (знак заряда  -точки) и поляризационного азимута (знак индекса
-точки) и поляризационного азимута (знак индекса  -точки) соответственно.
-точки) соответственно.
Дата добавления: 2015-07-12; просмотров: 74 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сети вихрей – скелетон фазы скалярного поля 2 страница | | | Сети вихрей – скелетон фазы скалярного поля 4 страница |