
Читайте также:
|
& Литература: [8], [3], [6].
Оператор момента импульса получается по сформулированному выше правилу из классического определения этой величины:
 = [
= [ 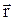
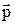 ]. →
]. → 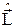 = [
= [ 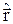

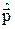 ]. (12.1)
]. (12.1)
Чтобы получить выражения для операторов проекций момента импульса, следует раскрыть векторное произведение (12.1):
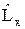 = y
= y 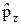 –z
–z 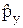 ,
, 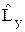 = z
= z 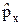 –x
–x 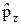 ,
, 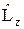 = x
= x 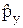 –y
–y 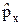 ,
, 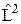 =
= 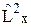 +
+ 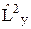 +
+ 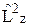 . (12.2)
. (12.2)
Полученные четыре оператора удовлетворяют таким перестановочным соотношениям: [ 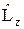
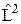 ] = 0, [
] = 0, [ 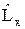
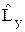 ] = i ħ
] = i ħ 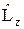 , (12.3)
, (12.3)
остальные получаются заменой x→y→z→x.
Из соотношений (12.3) следуют свойства момента импульса микрообъектов, которые не присущи классическим частицам. Проекции момента импульса не совместны, поэтому векторная величина момент импульса не имеет определенного направления в пространстве, ее нельзя изобразить направленным отрезком. Определенное значение имеют только квадрат момента импульс и его проекция на произвольно выбранное направление оси z. Для наглядного представления такой ситуации момент импульса изображают в определенном масштабе конусом, образующая которого равна 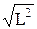 , а высота – Lz. Можно представлять себе, что образующая конуса быстро вращается (совершает прецессию) вокруг оси конуса.
, а высота – Lz. Можно представлять себе, что образующая конуса быстро вращается (совершает прецессию) вокруг оси конуса.
Еще одним следствием (12.3) является квантование момента импульса: L2 = ħ 2 l (l +1), Lz = ħ m, (12.4)
где l = 0, 1, 2,…– орбитальное квантовое число, а m = – l, – l +1, – l +2, …, l – магнитное квантовое число. Правила квантования можно получить не только из (12.3), но и из решения уравнения для собственных значений операторов 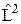 и
и 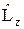 . Экспериментально квантование момента импульса было доказано в 1922 году опытами О. Штерна(1888–1968) и В. Герлаха (1889–1979).
. Экспериментально квантование момента импульса было доказано в 1922 году опытами О. Штерна(1888–1968) и В. Герлаха (1889–1979).
Классическая частица с зарядом q и массой m обладает магнитным моментом  , который пропорционален моменту импульса
, который пропорционален моменту импульса  :
:  = g
= g  . Величину g = q / (2 m) называют гиромагнитным отношением. Проверка связи магнитного момента с моментом импульса и измерение гиромагнитного отношения были целью опытов А. Эйнштейна и де Газа (1878–1960), проведенных в 1915 году. Пропорциональность магнитного момента моменту импульса подтвердили эти опыты, но гиромагнитное отношение оказалось отличным от величины q / (2 m). В опытах Штерна и Герлаха непосредственно наблюдалось квантование проекции магнитного момента, пропорционального моменту импульса. Пропорциональность величин Mz и Lz послужила поводом назвать квантовое число m магнитным квантовым числом.
. Величину g = q / (2 m) называют гиромагнитным отношением. Проверка связи магнитного момента с моментом импульса и измерение гиромагнитного отношения были целью опытов А. Эйнштейна и де Газа (1878–1960), проведенных в 1915 году. Пропорциональность магнитного момента моменту импульса подтвердили эти опыты, но гиромагнитное отношение оказалось отличным от величины q / (2 m). В опытах Штерна и Герлаха непосредственно наблюдалось квантование проекции магнитного момента, пропорционального моменту импульса. Пропорциональность величин Mz и Lz послужила поводом назвать квантовое число m магнитным квантовым числом.
? Контрольные вопросы
1. Запишите операторы момента импульса.
2. Запишите перестановочные соотношения для операторов момента импульса.
3. Расскажите о физических следствиях перестановочных соотношений для операторов моментов импульса?
4. Запишите правила квантования момента импульса.
5. Расскажите о связи магнитного момента и момента импульса.
|
Д. 12.1. Опыты Штерна и Герлаха.
12.1. Выведите коммутационные соотношения для операторов проекций момента импульса.
12.2. Выведите коммутационное соотношение для оператора квадрата момента импульса и оператора и его проекции на некоторое направление.
12.3. Докажите, что перестановочные соотношения для операторов суммы независимых моментов такие же как и для операторов каждого из них.
12.4. Докажите, что [ 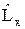 x] = 0, а [
x] = 0, а [ 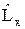 y] = i ħ z.
y] = i ħ z.
Спин
& Литература: [1], [8], [3], [6].
В отличие от классических частиц микрообъекты могут обладать отличным от нуля моментом импульса, даже если их импульс равен нулю. Момент импульса, не зависящий от импульса, получил название спинового момента, или спина. Гипотезу о наличии спина у электронов выдвинули в 1925 году С. Гаудсмит (1902–1979) и Дж. Уленбек (1900–1988) для объяснения дублетности спектральных линий щелочных металлов.
Экспериментальным доказательством наличия спина является обнаружение в опытах Штерна и Герлаха раздвоения в неоднородном магнитном поле атомарного пучка, состоящего из атомов с нулевым орбитальным моментом, на две части.
Правила квантования орбитального момента (12.4) распространяются и на спиновые моменты с изменением обозначений:
S2 = ħ 2 s (s+1), Sz = ħ s, (13.1)
где s = 1/2– спиновое квантовое число, а s = –1/2, 1/2 квантовое число проекции спина, или спиновая переменная. Число различных значений проекций момента в соответствии с (12. 4) равно 2 l + 1. Для спинового момента электрона это число 2 s +1 должно быть равным 2, чтобы обеспечить дублетность спектральных линий. Отсюда и получаются значения чисел s и s в (13.1). Спиновое квантовое число s отличных от электрона микрообъектов, например многоэлектронных атомов, может быть иным, например s = 0, 1, 3/2. Соответственно, s = –s, –s+1, –s+2, …, s.
Со спином заряженной частицы связан и пропорциональный ему спиновый магнитный момент: Msz = gs Sz. В отличие от орбитального спиновое гиромагнитное отношение gs в два раза больше: gs =2q / (2 m). Именно это является причинной отличия гиромагнитного отношения, полученного в опытах Эйнштейна и де Газа, от того, которое ожидалось.
Как учитывается спин при описании электрона? В набор переменных, от которых зависит амплитуда состояния Y, помимо других переменных B следует включить и проекцию спина на некоторое направление z или соответствующую спиновую переменную s: Y = Y(B, s). В нерелятивистском приближении амплитуду такого состояния можно представить в виде произведения двух частей: Y(B, s) = Y(B) Ys (s). Второй сомножитель – спиновая часть амплитуды состояния, или амплитуда спинового состояния. Эта амплитуда представляет собой совокупность лишь двух значений 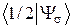 и
и 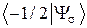 , которые можно рассматривать как проекции вектора ÷Ysñ на базисные векторы ÷1/2ñ и ÷–1/2ñ. Вектор ÷Ysñ называют вектором спинового состояния. Его можно обозначить и ÷ sñ, не забывая, что ось, относительно которой находится переменная s, может не совпадать с осью, относительно которой определены базисные векторы 1/2ñ и ÷–1/2ñ.
, которые можно рассматривать как проекции вектора ÷Ysñ на базисные векторы ÷1/2ñ и ÷–1/2ñ. Вектор ÷Ysñ называют вектором спинового состояния. Его можно обозначить и ÷ sñ, не забывая, что ось, относительно которой находится переменная s, может не совпадать с осью, относительно которой определены базисные векторы 1/2ñ и ÷–1/2ñ.
Операторы спина 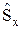 ,
, 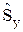 ,
, 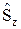 ,
, 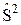 не могут быть, подобно операторам орбитального момента, выражены посредством операторов координат и импульсов, но другие свойства орбитального момента присущи и операторам спина. Операторы спина также должны быть самосопряженными и на них распространяются те же правила квантования (13.1) и те же перестановочные соотношения (12.3), что и для орбитального момента:
не могут быть, подобно операторам орбитального момента, выражены посредством операторов координат и импульсов, но другие свойства орбитального момента присущи и операторам спина. Операторы спина также должны быть самосопряженными и на них распространяются те же правила квантования (13.1) и те же перестановочные соотношения (12.3), что и для орбитального момента:
[ 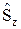
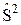 ] = 0, [
] = 0, [ 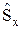
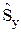 ] = i ħ
] = i ħ 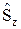 , (13.2)
, (13.2)
остальные получаются заменой x→y→z→x.
Требованиям, аналогичным операторам, должны удовлетворять и сопоставляемые им матрицы. В качестве базиса представления операторов спина берут собственные векторы ÷ sñ оператора 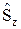 :
: 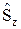 ÷ sñ = ÷ sñ sz. Этот базис является собственным не только для оператора
÷ sñ = ÷ sñ sz. Этот базис является собственным не только для оператора 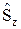 , но и для оператора
, но и для оператора 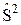 , поскольку данные операторы коммутируют. Поэтому матрицы операторов
, поскольку данные операторы коммутируют. Поэтому матрицы операторов 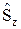 и
и 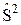 имеют диагональный вид:
имеют диагональный вид:
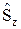 =
= 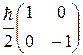 =
= 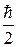 sz;
sz; 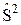 =
= 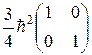 =
= 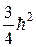 dik. (13.3)
dik. (13.3)
Для обозначения матриц используют те же символы, что и для обозначения соответствующих операторов.
Матрицы 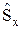 и
и 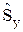 должны быть подобраны так, чтобы он были самосопряженными и чтобы для них выполнялись соотношения (13.2). Таковыми являются:
должны быть подобраны так, чтобы он были самосопряженными и чтобы для них выполнялись соотношения (13.2). Таковыми являются:
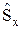 =
= 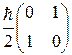 =
= 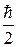 sx;
sx; 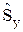 =
= 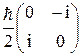 =
= 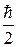 sy. (13.4)
sy. (13.4)
Величины sx, sy и sz, входящие в формулы (13.3) и (13.4), называют матрицами Паули.
? Контрольные вопросы
6. Что такое спин?
7. Как наличие спина проявлялось в опытах Штерна и Герлаха?
8. Расскажите о правилах квантования спина.
9. Как учитывается спин при описании состояния электрона?
10. Расскажите об амплитуде и векторе спинового состояния.
11. Какими свойствами обладают операторы спина?
12. Из каких соображений получаются матрицы операторов спина?
13. Какие операторы спина и почему имеют диагональный вид?
|
Д. 13.1. Спин электрона.
История появления понятия «спин». Экспериментальное обнаружение спина в опытах Штерна и Герлаха. Опыты Эйнштейна и де Газа.
13.1. Докажите, чтоматрицы спиновых операторов (13.3) и (13.4) эрмитовы и удовлетворяют соотношениям (13.2).
13.1. Докажите, что матрицы Паули удовлетворяют соотношению
sx2 + sy2 + sz2 = 3 dik.
Дата добавления: 2015-07-11; просмотров: 195 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Операторы координат, импульсов и их функций | | | Уравнение Шредингера. Стационарные состояния |