
Рассмогрим две операции, применяемые только к высказывательным формам. Эти опера-ции, гак называемые навешивания кванторов, будучи применёнными к высказывательной форме, приводят либо снова к высказывательной форме, либо к высказыванию.
Начнем с простейшего случая. Пусть  (х) – одноместная высказывательная форма; область значений переменной х обозначим буквой M. Обозначим через
(х) – одноместная высказывательная форма; область значений переменной х обозначим буквой M. Обозначим через
( х
х  M)
M)  (х), (2)
(х), (2)
или, если М ясно из контекста, через
( х)
х)  (х), (3)
(х), (3)
следующее высказывание: «для любого значения переменной х высказывание, полученное под-становкой имени этого значения в форму  (х) вместо х, истинно». Знак
(х) вместо х, истинно». Знак  называется кванто-ром общности, переход от формы
называется кванто-ром общности, переход от формы  (х) к высказываниям (2), (3) – навешиванием на форму
(х) к высказываниям (2), (3) – навешиванием на форму  (х) квантора общности по переменной х.
(х) квантора общности по переменной х.
Обозначим через
( х
х  M)
M)  (х), (4)
(х), (4)
или, если М ясно из контекста, через
( х)
х)  (х), (5)
(х), (5)
следующее высказывание: «существует такое значение переменной х, что высказывание, полу-ченное подстановкой имени этого значения в форму  (х) вместо х, истинно». Знак
(х) вместо х, истинно». Знак  называет-ся квантором существования, переход от формы
называет-ся квантором существования, переход от формы  (х) к высказываниям (4), (5) – навешивани-ем на форму квантора существования по переменной х.
(х) к высказываниям (4), (5) – навешивани-ем на форму квантора существования по переменной х.
Пример 12. Рассмотрим следующую высказывательную форму  (х): «Девочку в группе зовут Маша» с одной переменной «девочка». Областью значений переменной является множес-тво всех девочек из данной группы. Используя кванторы, получаем высказывания (не высказы-вательные формы!):
(х): «Девочку в группе зовут Маша» с одной переменной «девочка». Областью значений переменной является множес-тво всех девочек из данной группы. Используя кванторы, получаем высказывания (не высказы-вательные формы!):
«Всех девочек в группе зовут Маша»
«Некоторую девочку в группе зовут Маша»
«Ни одну девочку не зовут Маша», и т.п ■
Рассмотрим общий случай. Пусть  (x 1, …, xs) – s-местная высказывательная форма (s ≥ 2); область значений переменной xi – множество Мi (i = 1, …, s). В силу введённых выше обозначе-ний для любого i = 1, …, s выражения
(x 1, …, xs) – s-местная высказывательная форма (s ≥ 2); область значений переменной xi – множество Мi (i = 1, …, s). В силу введённых выше обозначе-ний для любого i = 1, …, s выражения
( хi
хi  M)
M)  (x 1, …, xs), (6)
(x 1, …, xs), (6)
( хi
хi  M)
M)  (x 1, …, xs) (7)
(x 1, …, xs) (7)
являются (s –1)-местными высказывательными формами, зависящими от переменных x 1, …, x i–1,
xi +1, …, xs Буква xi в выражениях (6), (7) называется связанной переменной, а все остальные пе-ременные, на которые не навешаны кванторы, называются в таких случаях свободными пере-менными. Сразу скажем, что свободные переменные – это просто переменные в смысле опре-деления из раздела 1. А связанные переменные переменными в этом смысле (т.е. буквами, вмес-то которых можно подставлять элементы из множества значений) вообще не являются. Всё, что можно с ними сделать: заменить букву, написанную сразу после квантора, и все вхождения этой буквы в рассматриваемую форму, на одну и ту же букву, отличную от имён всех осталь-ных переменных. Заметим, что близкий смысл имеет индекс суммирования i в суммах вида 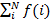 , переменная интегрирования t в интегралах
, переменная интегрирования t в интегралах 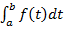 , переменная, по которой берётся максимум (или минимум):
, переменная, по которой берётся максимум (или минимум):  , и т.д. Общими во всех этих случаях являются два факта: 1) результат (сумма, интеграл, максимум и пр.) не зависит от этой связанной переменной, и 2) эту букву можно везде заменить на любую другую, не совпадающую с другими в данном выра-жении. Таким образом, можно сказать, что навешивание квантора по переменной х связывает эту переменную.
, и т.д. Общими во всех этих случаях являются два факта: 1) результат (сумма, интеграл, максимум и пр.) не зависит от этой связанной переменной, и 2) эту букву можно везде заменить на любую другую, не совпадающую с другими в данном выра-жении. Таким образом, можно сказать, что навешивание квантора по переменной х связывает эту переменную.
По определению квантора общности, высказывание
( хi
хi  M)
M)  (a 1, …, ai –1, xi, ai +1, …, as), (8)
(a 1, …, ai –1, xi, ai +1, …, as), (8)
истинно тогда и только тогда, когда для любого значения ai  Mi переменной xi высказывание
Mi переменной xi высказывание
 (a 1, …, ai –1, ai, ai +1, …, as) (9)
(a 1, …, ai –1, ai, ai +1, …, as) (9)
истинно.
По определению квантора существования высказывание
( хi
хi  M)
M)  (a 1, …, ai –1, xi, ai +1, …, as), (10)
(a 1, …, ai –1, xi, ai +1, …, as), (10)
истинно тогда и только тогда, когда существует такое значение ai  Mi переменной xi, что вы-сказывание
Mi переменной xi, что вы-сказывание
 (a 1, …, ai –1, ai, ai +1, …, as) (11)
(a 1, …, ai –1, ai, ai +1, …, as) (11)
истинно.
Задание 4. Проверить следующие равносильности
1. ( х)[
х)[  (х)
(х) 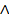
 (x)] º (
(x)] º ( х)
х)  (х)
(х) 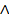 (
( х)
х)  (x)
(x)
2. ( х)[
х)[  (х)
(х) 
 (x)] º (
(x)] º ( х)
х)  (х)
(х)  (
( х)
х)  (x)
(x)
3. ( х)[
х)[  (х)
(х) 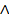
 (x)] º (
(x)] º ( х)
х)  (х)
(х) 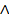 (
( х)
х)  (x)
(x)
4. ( х)[
х)[  (х)
(х) 
 (x)] º (
(x)] º ( х)
х)  (х)
(х)  (
( х)
х)  (x)
(x)
5. ( х)[
х)[  (х)→
(х)→  (x)] º (
(x)] º ( х)
х)  (х)→(
(х)→( х)
х)  (x)
(x)
6. ( х)[
х)[  (х)
(х) 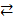
 (x)] º (
(x)] º ( х)
х)  (х)
(х) 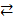 (
( х)
х)  (x)
(x)
7. ( х)[
х)[  (х)→
(х)→  (x)] º (
(x)] º ( х)
х)  (х)→(
(х)→( х)
х)  (x)
(x)
8. ( х)[
х)[  (х)
(х) 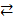
 (x)] º (
(x)] º ( х)
х)  (х)
(х) 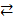 (
( х)
х)  (x) ■
(x) ■
С помощью кванторов можно ввести некоторые понятия, относящиеся к произвольным соответствиям (см. раздел 3-5). Пусть Г = á G, X, Y ñ – соответствие, А – множество. Образом А относительно Г называется и через Г (А) обозначается множество всех тех элементов из Y, каждый из которых соответствует в соответствии Г какому-нибудь элементу множества А. Таким образом,
Г (А) = { y Î Y | ( x Î А) á x, y ñÎ G }. (12a)
x Î А) á x, y ñÎ G }. (12a)
В формуле (12) выражение после знака | имеет такой же смысл, как в формуле (1). Оно является одноместной высказывательной формой, зависящей от переменной y с областью значений Y. В множество Г (А) входят все те элементы Y, для которых высказывательная форма ( x Î А)á x, y ñÎ G
x Î А)á x, y ñÎ G
истинна.
Если Г = á G, X, Y ñ – соответствие, А – множество, то полным прообразом А относитель-но Г называется и через Г –1(А) обозначается множество всех тех элементов из X, каждому из ко-торых соответствует в соответствии Г элемент множества А. Таким образом,
Г –1(А) = { x Î X | ( y Î А) á x, y ñÎ G }. (12b)
y Î А) á x, y ñÎ G }. (12b)
3.1. Отрицание высказываний с кванторами. Как и для любых высказываний, отрица-ние высказывательных форм, содержащих кванторы, является высказывательной формой или высказыванием с противоположным значением истинности. Если в высказывательной форме имеется ровно одна переменная, то после навешивания на неё кванторов (общности или сущес-твования) эта форма становится высказыванием – именно, высказыванием, содержащим кван-тор. Именно такие высказывания рассматриваются в данном разделе.
Пример 13. Вернёмся к 1-ому из высказываний из примера 12: «Всех девочек в группе зовут Маша». Отрицанием этого высказывания является высказывание «Некоторых девочек в группе не зовут Маша». Как обычно, то же самое утверждение может быть выражено различны-ми способами:
«Не всех девочек в группе зовут Маша»
«Неверно, что всех девочек в группе зовут Маша»
«По крайней мере одну девочку в группе не зовут Маша», и т.д ■
Пример 14. Рассмотрим высказывание «У некоторых кошек есть блохи». Поскольку «не-которые» в данном контексте значит «по меньшей мере, одна», высказывание «У некоторых ко-шек есть блохи» по смыслу совпадает с высказыванием «По меньшей мере, у одной кошки есть блохи». Отрицанием этого высказывания является «Ни у одной кошки нет блох», которое мо-жет быть записано также в виде «У всех кошек нет блох» ■
Обобщая рассуждения из примеров 13 и 14, можно прийти к следующей таблице, содер-жащей схемы для построения отрицаний высказываний с кванторами.
Таблица 1. Отрицания высказываний с кванторами
| Высказывание | Отрицание |
| Все делают (имеют и пр.) | Некоторые не делают (Эквивалентно: не все делают) |
| Некоторые дела-ют (имеют и пр.) | Никто не делает (Эквивалентно: все не делают) |
Отрицанием отрицания является само исходное высказывание. Как и все остальные высказыва-ния, они могут быть записаны в разном виде (см. таблицу 1).
Пример 15. Рассмотрим следующие изображения, разделённые на группы A, B, и C.

Отметим одной (или несколькими) буквами группу или группы картинок, удовлетворяющих условию «По меньшей мере хотя бы одна картинка из группы не имеет рамки». Группы A и B удовлетворяют этому условию, а группа C – нет ■
Задание 5. Написать отрицания следующих высказываний
1. У каждой собаки есть свой день
2. На равнинах Испании сегодня нет дождей
3. Некоторые книги длиннее, чем эта книга
4. Ни один мастер по ремонту компьютеров не умеет играть в «блэкджек»
5. Некоторым людям всегда везёт
6. Каждый иногда любит кого-то
7. Все любят победителя
8. Все мужчины созданы равными
9. Некоторые ученики из нашего класса ездили на загородную экскурсию ■
Задание 6. Для изображений из примера 15 отметить одной (или несколькими) буквами группу или группы картинок, удовлетворяющих условиям:
1. Ни одна картинка не имеет рамки
2. По меньшей мере одна картинка не имеет рамки
3. Не каждая картинка имеет рамку
4. По меньшей мере одна картинка имеет рамку
5. Нет картинок, которые не имеют рамки
6. Все картинки не имеют рамки
7. Не каждая картинка не имеет рамки ■
Дата добавления: 2015-10-16; просмотров: 120 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Высказывательные формы | | | Часть 2. ОПТИМИЗАЦИЯ НА ГРАФАХ |