Відомі різновиди та узагальнення кривої Пеано

В попередньому підрозділі ми визначили розмірність кривої Пеано, але як виявилось існує спосіб побудови кривої Пеано розмірності 3. На першому етапі побудови об’єкт розмірності 3 – куб розбивається на вісім кубиків і крива Пеано на першому етапі побудови буде мати вигляд, який показано на рис. 4.4.

Рис. 4.4.

Тобто крива Пеано буде обходити кожен кубик, на які розбивається великий куб, по одному з ребер. Аналогічний спосіб обходу чотирикутника по стороні був запропонований Гілбертом, на відміну способу обходу по діагоналі, що був запропонований Пеано. Тобто можна аналогічно показати спосіб обходу по діагоналі для куба.

Можна також уявити собі криву “Пеано” для трикутника. Нехай нам даний довільний рівносторонній трикутник. Розіб'ємо трикутник, як і квадрат, на чотири подібних йому трикутники. Це можна зробити хоча б таким способом (рис 4.5):

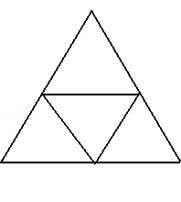
Рис. 4.5.

Назвемо ці трикутники трикутниками першого рангу. Пронумеруємо їх (рис. 4.6):

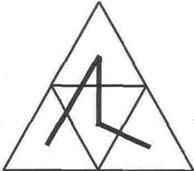
Рис. 4.6.

Аналогічно, так як і в квадраті, розіб'ємо отримані трикутники іще на чотири частини. Після такого розбиття ми матимемо шістнадцять трикутників другого рангу (рис 4.7).

Рис. 4.7.

Далі кожен з трикутників другого рангу ми знов розіб'ємо на чотири трикутники і таким чином отримаємо 64 трикутники третього рангу (рис.4.8).

Рис. 4.8.

Цей процес розбивки трикутників ми можемо продовжувати безмежно; при цьому зі зростанням номера рангу розбивки сторони трикутників будуть наближатися до нуля. Тому, аналогічно, ми отримаємо неперервне відображення відрізка на трикутник.

Наведемо ще один приклад кривої “Пеано”, тепер уже для трьох вимірної фігури — для куба. Вона задасть відображення відрізку на куб. Будемо розбивати куб, так як і квадрат, на подібні йому куби, нумеруючи їх при цьому. Нам лише треба слідкувати за тим щоб сусідні два куби мали принаймні хоча б одну спільну точку. Це нам потрібно для того щоб створене нами відображення було неперервним (крива не розривалася). Ми можемо цього досягти якщо будемо розбивати куб площинами паралельними до його граней, рівновіддаленими від них. В процесі такої розбивки ми отримаємо вісім кубів що матимуть одну спільну точку, центр куба. Потім кожен з цих кубів ми також розбиватимемо на куби і так далі, нумеруючи їх таким чином, щоб сусідні мали хоча б одну спільну точку. Цей процес будемо продовжувати до нескінченності.

До тепер ми розглядали лише звичні об'єкти, які лише з певним ступенем припущення можна назвати фракталами. Квадрат можна розбити на чотири подібних квадрати, трикутник, також на подібні йому складові. Хотілося б, щоб крива “Пеано” заповнювала який не будь об'єкт, що має фрактальну структуру. Після проведення дослідження в цьому напрямку, було виявлено що це цілком можливо.

Для досліджень нами було взято найвідоміший та найпопулярніший фрактал – сніжинку Коха. Використавши результати С. В. Нечипоренка [16], було виявлено що сніжинка Коха може бути розбита на сім, подібних їй самій, сніжинка Кохa. Яким чином це відбувається? Відповідь на дане питання описана в розділі 2.

Отже, робимо висновок, що одну зірку можна розбити на 7, трішки меншими розмірами і які не залишатимуть між собою не покритих місць (рис. 4.9).

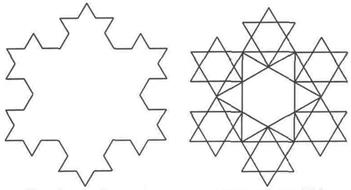
Рис. 4.9.

Цей спосіб розбиття цілком задовольняє умови, які потрібні для побудови кривої “Пеано”. Звичайно могли виникнути проблеми з умовою, щоб сусідні дві зірки мали принаймні хоча б одну спільну точку. Але при запропонованій нумерації таких не виникає.

Будемо зображати зірку трикутником [22], для спрощення малюнку, та проілюструємо перший крок побудови кривої (рис. 4.10).

Рис. 4.10.

Як бачимо при такому способі обходу кожні дві сусідні зірки Коха, крім четвертої та п'ятої, все ж таки мають одну спільну точку, в четвертої та п'ятої їх взагалі безліч. Для нашої кривої цієї точки досить щоб перейти від одної зірки до наступної. Отже таким чином ми задали правило обходу зірки кривою, а це означає що ця крива заповнить всю зірку. Нижче зображено другий (рис. 4.11(а)) та третій (рис. 4.11(б)) кроки побудови.

Рис. 4.11(а).

Рис. 4.11(б).

Дата добавления: 2015-08-21