Острівець Коха та його властивості

Означення 4. Острівцем Коха називається сніжинка Коха разом із частиною площини, яку вона обмежує (рис 2.5).

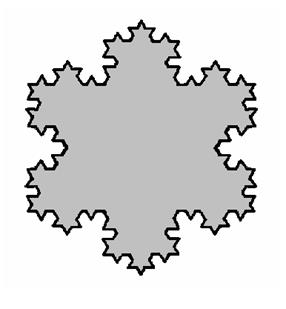
Рис 2.5.

Властивість 1. До острівця Коха можна приєднати шість острівців Коха, які подібні до початкового з коефіцієнтом подібності , так, що між ними не залишиться точок, які не належать жодному острівцю Коха.

Доведення. Цей факт випливає з наслідку із властивості 4 сніжинки Коха [2].

Наслідок. Острівець Коха розпадається на 7 острівців (рис. 2.6), причому центральний острівець подібний до великого з коефіцієнтом подібності , а решта шість – з коефіцієнтом подібності .

Властивість 2. Острівець Коха є самоподібною фігурою розмірності два.

Доведення. Згідно з вище наведеним наслідком, острівець Коха можна розбити на сім острівців (рис. 2.6).

Рис 2.6.

Більший з одержаних острівців подібний до початкового острівця із коефіцієнтом подібності . Дійсно, нехай діаметр початкового острівця Коха дорівнює два, тобто 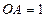. Згідно з властивістю сніжинки Коха, більший з отриманих острівців подібний до початкового острівця. Для знаходження коефіцієнту подібності знайдемо відношення півдіаметрів цих острівців Коха. Легко видно, що трикутник правильний, , тому OD=1/2, Звідси . Отже .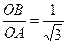

Згідно з вище наведеним наслідком, менші з одержаних острівців подібні до більшого острівця з коефіцієнтом подібності , тому вони подібні до початкового острівця з коефіцієнтом подібності . Складаємо рівняння , з якого і знаходимо розмірність самоподібності острівця Коха . Доведено.

Властивість 3. Існує неперервна крива, яка проходить через усі точки острівця Коха [2].

Доведення. На першому етапі розіб’ємо острівець Коха на сім острівців і пронумеруємо отримані острівці цифрами від 0 до 6 (рис. 2.7). Поставимо у відповідність кожному острівцю відрізок довжини 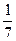(рис. 2.8). Так острівцю з номером 0 відповідатиме відрізок [0; 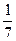], острівцю з номером 1 відповідатиме відрізок [ 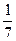; ] і т.д. Перейшовши до сімкової системи числення, отримаємо відповідність:

острівцю з номером 0 – відрізок [0; 0,1₇],

острівцю з номером 1 – відрізок [0,1₇; 0,2₇],

острівцю з номером 2 – відрізок [0,2₇; 0,3₇],

...

острівцю з номером 6 – відрізок [0,6₇; 1].

На другому етапі кожен із острівців знову розбиваємо на 7 острівців, а кожен з відрізків на 7 відрізків і знову встановлюємо відповідність між острівцями і відрізками.

Острівцю з номером 00 відповідає відрізок [0; 0,01₇],

острівцю з номером 01 відповідає відрізок [0,01₇; 0,02₇],

...

острівцю з номером 66 відповідає відрізок [0,66₇; 1].

Процес розбиття острівця на сім острівців можна продовжувати нескінченно, тому отримаємо відображення острівця Коха на відрізок [0;1]. При цьому кожній точці острівця відповідає деяка (можливо не єдина) точка відрізка [0;1]. Справді, візьмемо довільну точку Х острівця Коха і побудуємо для неї послідовність вкладених острівців, що містять точку Х. Ця послідовність задовольняє умови теореми про вкладені замкнені множини [7:70], і тому існує єдина точка (це точка Х), яка належить всім членам послідовності вкладених острівців. Для цієї послідовності острівців існує послідовність відповідних відрізків, яка в свою чергу задовольняє умовам теореми Кантора про вкладені відрізки [7]. Тому існує єдина точка на відрізку [0;1], яка відповідає точці Х.

Таким чином, можна побудувати неперервну криву, яка за одиничний відрізок часу пройде через усі точки острівця Коха. Доведено.

Рис. 2.7.

Рис. 2.8.

З властивості 3 слідує, що використовуючи генератор (рис. 2.9) на другому кроці побудови отримаємо певну криву (рис. 2.10) [13:104], а на п -ому кроці побудови отримаємо острівець Коха.

Рис. 2.9. Рис. 2.10.

Дата добавления: 2015-08-21