
|
Читайте также: |
I. Рассмотрим произвольную последовательность {xn}, а=  xn и пусть
xn и пусть  В
В  n, n=1, 2, …: xn
n, n=1, 2, …: xn  В.
В.
Предположим противное: а>В.
Так как 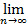 xn=а
xn=а 
 >0, а значит и для
>0, а значит и для  =а-В>0,
=а-В>0,  N
N  n>N: │xn - а│<а-В
n>N: │xn - а│<а-В  -а+В+а<xn<а-В+а
-а+В+а<xn<а-В+а  В<xn <2а-В
В<xn <2а-В
Мы пришли к противоречию с тем, что  : xn
: xn  В.
В.
II. Рассмотрим произвольную последовательность {xn}, а=  xn, для которой существует А такое, что
xn, для которой существует А такое, что  : xn
: xn  А
А  -xn
-xn  -А
-А
Тогда для последовательности {-xn} выполняется  (-xn)= -а и для каждого n, n=1, 2, …: -xn
(-xn)= -а и для каждого n, n=1, 2, …: -xn  -А. Согласно п. I -а
-А. Согласно п. I -а  -А
-А 
 .
.
Замечание.
Если в условиях теоремы 1 неравенство строгое, то в утверждении теоремы 1 следует сохранить нестрогие неравенства а  В (соответственно, а
В (соответственно, а  А).
А).
Пример.
{xn}={  }.
}.  n:
n:  >0
>0
Но  =0.
=0.

Пусть {xn} такова, что 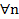 : А
: А  xn
xn  В и
В и  xn=а.
xn=а.
Тогда А  а
а  В.
В.
Указанное свойство отрезка [А, В] называется свойством замкнутости, то есть если на отрезке располагается сходящаяся последовательность, то отрезок не выпустит за свои границы предел этой последовательности.
Интервал (А, В) таким свойством не обладает.
Следствие 2.
Если последовательности {xn} и {yn} сходятся, причём  xn=а,
xn=а,  yn=b и
yn=b и 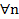 , n=1, 2, …: xn
, n=1, 2, …: xn  yn, то а
yn, то а  b.
b.
Доказательство.
Рассмотрим {yn-xn}. 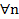 : yn-xn
: yn-xn  0. Согласно теореме 3 §2
0. Согласно теореме 3 §2  (yn-xn)=b-а, а согласно теореме 1 §4 b-а
(yn-xn)=b-а, а согласно теореме 1 §4 b-а  0
0  а
а  b.
b.
Теорема 2. (о трёх последовательностях)
Пусть {xn}, {yn} и {zn} таковы, что: 1) 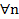 : xn
: xn  zn
zn  yn
yn
2)  xn=
xn= 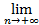 yn=а
yn=а
Тогда {zn} сходится и  zn=а.
zn=а.
Доказательство.
 xn=а
xn=а 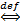
 0
0  N1
N1 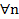 >N1: │xn - а│<
>N1: │xn - а│< 
 а-
а-  <xn<а+
<xn<а+ 
 yn=а
yn=а 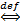
 >0
>0  N2
N2 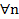 >N2: │yn - а│<
>N2: │yn - а│< 
 а-
а-  yn<а+
yn<а+ 
Возьмём произвольной  0 и положим N=max{N1, N2}.
0 и положим N=max{N1, N2}.
Тогда 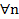 >N:
>N: 

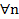 >N: а-
>N: а-  <xn
<xn  zn
zn  yn<а+
yn<а+ 
 а-
а-  < zn<а+
< zn<а+ 
Следовательно, 
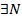
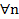 >N: │zn - а│<
>N: │zn - а│< 

 zn =а.
zn =а.
§5. Бесконечно большие последовательности.
(последовательности, стремящиеся к -  , к +
, к +  , к
, к  )
)
Определение.
Говорят, что числовая последовательность {xn} стремится к +  (к -
(к -  ), если
), если  E>0
E>0  N
N  n>N: xn>E (соответственно, xn<-E) и пишут
n>N: xn>E (соответственно, xn<-E) и пишут  xn=+
xn=+  (соответственно,
(соответственно, 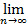 xn=-
xn=-  ).
).
Определение.
Говорят, что последовательность {xn} стремится к  , если
, если  >0
>0  N
N  n>N: │xn│>E и пишут
n>N: │xn│>E и пишут  xn=
xn= 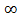 .
.
Замечание.
Общее название таких последовательностей – бесконечно большие.
Примеры.
1. {1, 2, …, n, …} стремится к + 
2. {-1, -4, -9, …, -n2, …} стремится к - 
3. {2, 1, 4, 3, …, 2k, 2k-1, …} стремится к + 
4. {1, -2, 3, -4, …, 2k-1, -2k, …} стремится к  , но не стремится ни к +
, но не стремится ни к +  , ни к -
, ни к -  .
.
Замечание.
Неограниченные последовательности, вообще говоря, не стремятся ни к +  , ни к -
, ни к -  , ни к
, ни к  …
…
Но тем не менее справедлива следующая теорема.
Теорема.
Любая неограниченная сверху (неограниченная снизу) возрастающая (соответственно, убывающая) последовательность стремится к +  (соответственно, к -
(соответственно, к -  ).
).
Дата добавления: 2015-10-30; просмотров: 138 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Закон двойственности. | | | Доказательство. |