|
Читайте также: |
Воспользуемся рабочей формулой определения точной верхней грани множества X.
Проверим выполнение двух условий.
(1) По определению наибольшего элемента для любого x 
: x 
.
(2) Возьмём произвольное 
>0, фиксируем его.
Тогда 
, а 
.
Утверждение для наименьшего элемента докажите самостоятельно.
Теорема 1. (О существовании точной верхней грани у ограниченного сверху числового множества)
Любое непустое ограниченное сверху числовое множество имеет точную верхнюю грань.
Доказательство.
Пусть X 
, X 
и существует В такое, что для любого x : x 
В.
Рассмотрим множество E всех чисел, ограничивающих множество X сверху.
E , так как В 
E. Следовательно, мы имеем два множества X и E, обладающих свойством:
X , E и для каждого x и для каждого В E x В.
А тогда согласно аксиоме V (полноты и непрерывности) множества 
действительных чисел существует Во 
такое, что для любого x и для любого В E
x Во В.
Из левой части неравенства x Во следует, что для любого x : x Во 
Во ограничивает множество X сверху Во E.
Из правой части неравенства следует, что для любого В E: Во В, а так как Во E, то Во – наименьшее из чисел, ограничивающих множество X сверху
Во= supX.
Доказательство, приведённое выше, принадлежит М.А.Крейнесу.
Теорема 2. (О существовании точной нижней грани у ограниченного снизу числового множества).
Любое непустое ограниченное снизу числовое множество имеет точную нижнюю грань.
Доказательство.
Пусть 
, 
и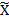 
– ограниченно снизу, то есть существует А такое, что для любого x 
: А x.
Рассмотрим множество X={-x; x }. Тогда для любого -x : - x -А, то есть множество X ограничено сверху и согласно теореме 1 существует Во= sup X 
для любого x : x Во -x 
- Во - Во= inf 
Глава 2.Числовые последовательности.
§1. Понятие числовой последовательности.
Рассмотрим произвольное число a (а – фиксировано) и произвольное число r , r>0.
Определение.
r- окрестностью или окрестностью точки а радиуса r называется множество (а- r, а+ r) 
, где
(а- r, а+ r)={x; x : 
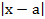<r}={ x; x : a-r<x<a+r}
Что такое последовательность?
(1) 1, 1, 1, …, 1, …
(2) 1, 2, 3, …, n, …
(3) -1, -2, -3, …, -n, …
(4) 0, 1, -1, 2, -2, …, k, -k, …
(5) 0, 1, 0, 1, …
(6) 1, 
, 
, …, 
, …
(7) , 0, , 0, 
, 0, …, 
, 0, 
, …
(8) 
1, 0, 2, …, 0, k, 0, …
(9) , 
, , 
, …, , , …
(10) , , 
, …, 
, …
Определение.
Говорят, что задана числовая последовательность, если указан закон, согласно которому каждому натуральному числу n поставлено в соответствие число xn.
Замечание.
Иногда полезно бывает допустить n=0, в других случаях целесообразно считать, что n принимает все положительные целые значения, начиная с nо, то есть n=nо, nо+1, nо+2, …, nо - целое, nо>0.
Будем обозначать последовательность
{x1, x2, …, xn, …}={ xn}
{ xn} 
или { xn} 
Определение.
Числовая последовательность (1) называется ограниченной сверху (снизу), если существует число В такое, что для любого n (n=1, 2, …): xn В (соответственно существует число А такое, что для любого n (n=1, 2, …): xn А).
Определение.
Последовательность (1) называется ограниченной, если она ограничена и сверху и снизу.
Определение.
Числовая последовательность (1) называется возрастающей (убывающей), если для любого n, n=1, 2, …: xn xn+1 (соответственно xn xn+1)
Определение.
Числовая последовательность (1) называется монотонной, если она либо возрастающая, либо убывающая.
Определение.
Последовательность (1) называется строго возрастающей (строго убывающей), если для любого n (n=1, 2, …): xn<xn+1 (соответственно xn>xn+1).
Общее название для строго возрастающей и строго убывающей последовательностей – строго монотонные.
Определение.
Число а называется пределом последовательности (1), если для каждого положительного числа 
>0) существует натуральное число (номер) N такое, что для любого номера n>N:
│xn-a│ 
или - 
< xn-а< 
а- < xn< 
xn 
(а- 
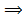, а+ )
| a-ε a a+ ε |
(а где расположены x1, x2, …, xN?)
Предел последовательности (1) обозначается: а= 
xn.
Определение.
Числовая последовательность называется сходящейся, если она имеет предел, то есть если существует число а такое, что а= xn 
существует а такое, что для каждого >0 существует номер N такой, что для каждого номера n>N: │xn-a│ .
Определение.
Последовательность (1) {xn } называется расходящейся, если она не имеет предела; если какое бы число а не взять существует о ( о>0) такое, что для каждого номера N существует номер nо>N такой, что │xno-a│ 
о.
§2. Бесконечно малые последовательности.
Среди всех сходящихся последовательностей особую роль играют последовательности, сходящиеся к нулю, то есть такие, что 0=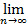 
xn.
Определение.
0= xn 
для каждого >0 существует номер N такой, что для каждого номера n>N: │xn│< xn (- , ).
Определение.
Последовательность, сходящаяся к нулю, называется бесконечно малой (б.м.).
Пример.
{1, , , …, 
, …}={ } 
Докажем, что 
.
Возьмём произвольное >0 и зафиксируем его. Ищем N такое, что для любого номера n>N: < .
Положим N= 
+1.
|
|
 +1
|
Возьмём произвольный номер n>N= +1 n> 
< . Что и требовалось доказать.
Задача 1.
Пусть q – произвольной действительное число, │q│<1.
Рассмотрим последовательность {1, q, q2, …, qn, …}={qn}
Доказать, что qn=0.
Задача 2.
Доказать, что любая бесконечная десятичная дробь является пределом последовательности своих десятичных приближений.
Теорема 1.
Для того, чтобы последовательность (1) { xn} сходилась к числу а необходимо и достаточно, чтобы для любого номера n, n=1, 2, …: xn=а+ 
n, где последовательность { n} б.м.
Дата добавления: 2015-10-30; просмотров: 176 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Простейшие операции над множествами. | | | Доказательство. |