
|
Читайте также: |
Теорема 14.8. Если функции  непрерывны вместе со своими частными производными первого порядка в некоторой замкнутой ограниченной поверхностно односвязной области V, то равносильны следующие четыре утверждения:
непрерывны вместе со своими частными производными первого порядка в некоторой замкнутой ограниченной поверхностно односвязной области V, то равносильны следующие четыре утверждения:
1)  , где l – замкнутый контур, лежащий внутри V;
, где l – замкнутый контур, лежащий внутри V;
2) 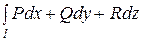 не зависит от выбора пути интегрирования;
не зависит от выбора пути интегрирования;
3)  есть полный дифференциал некоторой однозначной функции
есть полный дифференциал некоторой однозначной функции  , заданной в точках V;
, заданной в точках V;
4) выполняются равенства:  .
.
Функция  может быть найдена, например, по формуле
может быть найдена, например, по формуле
 (5.7)
(5.7)
где  - некоторая фиксированная точка области V, c – произвольная постоянная.
- некоторая фиксированная точка области V, c – произвольная постоянная.
Связь между КИ-1 и КИ-2. Пусть спрямляемая (не имеющая особых точек) линия AB имеет в каждой точке касательную, положительное направление которой составляет с осью координат углы  . Тогда
. Тогда
 .
.
Связь КИ-2 с двойным интегралом (формула Грина). Теорема 14.9. Пусть: 1) функции  непрерывны и имеют непрерывные частные производные в открытой односвязной области
непрерывны и имеют непрерывные частные производные в открытой односвязной области  ; 2) l – кусочно-гладкий контур, ограничивающий область
; 2) l – кусочно-гладкий контур, ограничивающий область  , и при положительном обходе l ближайшая часть области S находится слева от наблюдателя. Тогда справедлива формула:
, и при положительном обходе l ближайшая часть области S находится слева от наблюдателя. Тогда справедлива формула:
 .
.
Площадь плоской области. Площадь s фигуры S, ограниченной простым кусочно-гладким контуром l, равна
 .
.
Пример 20. Вычислить КИ-2:  , где L – дуга параболы
, где L – дуга параболы 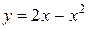 , проходимая от точки
, проходимая от точки  до точки
до точки  .
.
 Ñ Кривая l представлена на рис.14.24.
Ñ Кривая l представлена на рис.14.24.
|
 =
=  =
=  . #
. #
 Пример 21. Вычислить КИ-2:
Пример 21. Вычислить КИ-2:  , где l – замкнутый контур, полученный пересечением сферы
, где l – замкнутый контур, полученный пересечением сферы 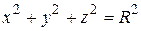 и цилиндра
и цилиндра 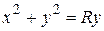
 , обходимый против часовой стрелки, если смотреть из начала координат (рис.14.25).
, обходимый против часовой стрелки, если смотреть из начала координат (рис.14.25).
|
 запишем в виде
запишем в виде 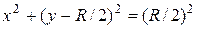 .Последнее равенство выполнится тождественно, если положить, например,
.Последнее равенство выполнится тождественно, если положить, например, 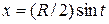 ,
,  ,
, 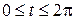 . Тогда из уравнения сферы имеем
. Тогда из уравнения сферы имеем  = =
= = 
 = =
= = 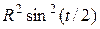 . Отсюда, помня, что
. Отсюда, помня, что 
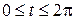 , имеем
, имеем  . Итак,
. Итак,  ;
;  ,
,  ,
,  . По формуле (5.5)
. По формуле (5.5)  =
= 

=  .#
.#
Пример 22. Найти первообразную функции  , если
, если  .
.
Ñ По формуле (5.7) при  получим
получим 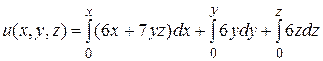

 .#
.#
Задачи для самостоятельного решения
Вычислить криволинейные интегралы второго рода:
97.  , где l – отрезок прямой
, где l – отрезок прямой 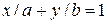 от точки пересечения ее с осью Ox до точки пересечения с осью Oy.
от точки пересечения ее с осью Ox до точки пересечения с осью Oy.
98.  , где l – контур прямоугольника с вершинами
, где l – контур прямоугольника с вершинами 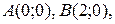
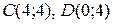 , указанными в порядке обхода l.
, указанными в порядке обхода l.
99.  вдоль линий: 1)
вдоль линий: 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  .
.
100.  , l – эллипс
, l – эллипс  , обходимый в положительном направлении.
, обходимый в положительном направлении.
101. 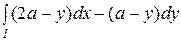 , где l – первая от начала координат арки циклоиды
, где l – первая от начала координат арки циклоиды  ,
,  .
.
102.  , где l – отрезок прямой от точки (1;1;1) до точки (2;3;4).
, где l – отрезок прямой от точки (1;1;1) до точки (2;3;4).
103. 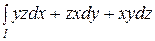 , где l – дуга винтовой линии
, где l – дуга винтовой линии 
 .
.
104.  , где l – линия пересечения сферы
, где l – линия пересечения сферы 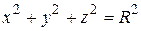 и цилиндра
и цилиндра  (
( ), обходимая против часовой стрелки, если смотреть из начала координат (часть кривой Вивиани).
), обходимая против часовой стрелки, если смотреть из начала координат (часть кривой Вивиани).
Убедиться, что подынтегральное выражение является полным дифференциалом, и вычислить КИ-2:
105.  . 106.
. 106.  . 107.
. 107.  .
.
108.  (контурное интегрирование не пересекает поверхность
(контурное интегрирование не пересекает поверхность  .
.
Найти первообразную функцию и по полному дифференциалу:
109.  .
.
110.  .
.
111. 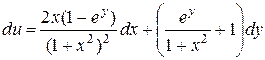 .
.
112.  .
.
113.  . 114.
. 114. 
С помощью формулы Грина вычислить КИ-2:
115.  , где l – окружность
, где l – окружность 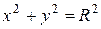 .
.
116.  , где l – эллипс
, где l – эллипс  .
.
117. Вычислить  , где l – простой замкнутый контур, пробегаемый в положительном направлении. Указание. Рассмотреть случаи: 1) начало координат находится вне контура l; 2) контур l окружает начало координат.
, где l – простой замкнутый контур, пробегаемый в положительном направлении. Указание. Рассмотреть случаи: 1) начало координат находится вне контура l; 2) контур l окружает начало координат.
118. В каждой точке эллипса 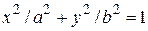 приложена сила
приложена сила  , равная по величине расстоянию от точки M до центра эллипса и направленная к центру эллипса. Найти работу
, равная по величине расстоянию от точки M до центра эллипса и направленная к центру эллипса. Найти работу  при перемещении в положительном направлении: а) вдоль дуги эллипса в первом октанте; б) вдоль всего эллипса.
при перемещении в положительном направлении: а) вдоль дуги эллипса в первом октанте; б) вдоль всего эллипса.
119. Сила по величине обратно пропорциональна расстоянию точки ее приложения от оси Oz, перпендикулярна к этой оси и направлена к ней. Найти работу этой силы по окружности  от точки
от точки 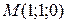 до точки
до точки  . Указание.
. Указание.  .
.
Дата добавления: 2015-10-30; просмотров: 104 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи для самостоятельного решения | | | Поверхностный интеграл первого рода (ПИ-1) |