
Читайте также:
|
Рассмотрим систему 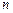 линейных уравнений с
линейных уравнений с 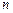 неизвестными
неизвестными  . Матрица
. Матрица  является квадратной. Ее определитель
является квадратной. Ее определитель  называется определителем системы. Заменим в определителе
называется определителем системы. Заменим в определителе 
 й столбец на столбец свободных членов
й столбец на столбец свободных членов  и обозначим получившийся определитель через
и обозначим получившийся определитель через  :
:
 .
.
Правило Крамера. Если определитель  квадратной системы отличен от нуля, то система совместна и имеет единственное решение, которое находится по формулам Крамера
квадратной системы отличен от нуля, то система совместна и имеет единственное решение, которое находится по формулам Крамера
 .
.
Заметим, что базисная система уравнений относительно главных неизвестных при фиксированных значениях свободных переменных может быть решена по правилу Крамера. Каждому набору свободных неизвестных будет соответствовать единственный набор главных неизвестных.
Правило Крамера применимо только к решению квадратных систем с невырожденной матрицей. Равенство нулю  не означает, что система не совместна. К решению таких систем следует применять другие методы, например, метод Гаусса. Отметим так же, что пользоваться формулами Крамера имеет смысл при решении систем небольшого порядка, иначе возникают трудности с вычислением определителей.
не означает, что система не совместна. К решению таких систем следует применять другие методы, например, метод Гаусса. Отметим так же, что пользоваться формулами Крамера имеет смысл при решении систем небольшого порядка, иначе возникают трудности с вычислением определителей.
Пример. Решить систему уравнений:

Определитель системы
 ,
,
поэтому система совместна и имеет единственное решение. Определители  :
:

Тогда 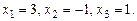
Метод Гаусса
Идея метода Гаусса состоит в том, что путем последовательного исключения неизвестных система уравнений превращается в ступенчатую (в частности, треугольную) эквивалентную систему уравнений.
Ступенчатой системой называется система вида

где  и
и  . При
. При 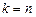 получаем треугольную систему. Очевидно, что треугольная система имеет единственное решение. Если
получаем треугольную систему. Очевидно, что треугольная система имеет единственное решение. Если  , то система уравнений является неопределенной. При этом
, то система уравнений является неопределенной. При этом 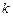 первых переменных можно принять за главные, а остальные за свободные неизвестные.
первых переменных можно принять за главные, а остальные за свободные неизвестные.
Для приведения системы уравнений к ступенчатому виду используются следующие преобразования, переводящие систему в эквивалентную:
1) перестановка любых двух уравнений,
2) умножение обеих частей уравнений на одно и тоже число,
3) прибавление к обеим частям уравнения соответствующих частей другого уравнения.
В результате таких преобразований получается или совместная ступенчатая система, эквивалентная исходной, или несовместная ступенчатая система. Несовместной будет система, в которой одно из уравнений имеет в правой части отличный от нуля свободный член, а коэффициенты в левой части равны нулю. В этом случае исходная система также несовместна.
При решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему, а ее расширенную матрицу, выполняя все преобразования над ее строками.
Пример. Решить методом Гаусса систему уравнений
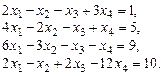
Выпишем расширенную матрицу системы. Умножая первую строку матрицы соответственно на 2, 3, 1, вычтем ее из второй, третьей и четвертой строк:
 .
.
Умножим вторую строку на 2 и 3 и вычтем ее из третьей и четвертой. В итоге получим матрицу
 .
.
Таким образом, эквивалентная ступенчатая система имеет вид

За главные неизвестные можно принять  и
и  , а за свободные
, а за свободные 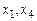 . Выражая главные через свободные, получим
. Выражая главные через свободные, получим

Поэтому общее решение нашей системы есть вектор – столбец

где свободные переменные 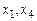 могут принимать любые значения.
могут принимать любые значения.
Задачи
Решить системы уравнений с помощью правила Крамера.
1.  2.
2. 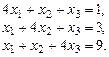
3.  3.
3. 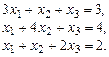
5.  6.
6. 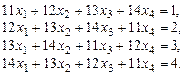
Решить системы уравнений методом Гаусса.
7.  8.
8. 
9.  10.
10. 
11. 
12. 
Дата добавления: 2015-10-26; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные определения | | | Однородные линейные системы |