Теорема Чебишева.

Нехай х₁, х₂, …х_n – випадкові величини, послідовні, попарно незалежні, які задовольняють умови: М(х_і) = а_і, D(х) ≤ с, і = 1, 2, …n.

.

58. Теорема Бернуллі.

Якщо ймовірність появи випадкової події А в кожному з n незалежних експериментів є величиною сталою і дорівнює р, то при необмеженому збільшенні числа експериментів n ® ¥ імовірність відхилення відносної частоти появи випадкової події W (A) від імовірності р, взятої за абсолютною величиною на e (e > 0) прямуватиме до одиниці зі зростанням n, що можна записати так:

Числові характеристики Х_і: M (X_i) = p; D (X_i) = M (X ² _i) – M ²(X_i) = p – p ² = p (1 – p) = pq.

Нерівність Чебишова для теореми Бернуллі матиме такий вигляд: ,

59. Центральна гранична теорема теорії ймовірностей (теорема Ляпунова) та її використання у математичній статистиці.

Теорема. Нехай задано n незалежних випадкових величин Х ₁, Х ₂, … Х_n, кожна із яких має один і той самий закон розподілу ймовірностей із M (Х_i) = 0, s (Х) = s і при цьому існує за абсолютною величиною початковий момент третього порядку , тоді зі зростанням числа n закон розподілу наближатиметься до нормального.

.

Таким чином, доведено, що характеристична функція випадкової величини Z при n ® ¥ дорівнює характеристичній функції нормованого нормального закону, а звідси випливає, що Z і пов’язана лінійною залежністю величина Y наближатимуться до нормального закону розподілу.

При досить загальних умовах розподіл суми великого числа незалежних випадкових величин близький до нормального розподілу.

60. Предмет і задачі математичної статистики.

Мета кожного наукового дослідження – виявлення закономірностей явищ, які спостерігають та використання цих закономірностей у практичній діяльності. Для встановлення цих закономірностей у практичній діяльності проводять спеціальні дослідження та спостерігають одиничні явища. Далі роблять узагальнюючі висновки у вигляді закону.

Предмет математичної статистики полягає у розробці методів збору та обробки статистичних даних для одержання наукових та практичних висновків.

Задачі матем статистики:

- Вказати методи, способи збору та формування статистичних відомостей;

- Встановити закон розподілу ВВ або системи ВВ за статистичними даними;

- Визначити невідомі параметри розподілу;

- Перевірити правдоподібність припущень про закон розподілу ВВ, про форму зв’язку між ВВ.

61. Утворення вибірки. Генеральна та вибіркова сукупність.

Нехай потрібно вивчити сукупність об’єктів відносно деякої якісної або кількісної ознаки, які характеризують ці об’єкти. Розглядаючи одну ознаку припускають, що інші ознаки рівноправні або множина об’єктів однорідна, такі множини однорідних об’єктів назив статистичною сукупністю.

Наприклад: якщо дослідити партію деталей якісною ознакою, буде: стандартність або нестандартність кожної деталі; кількісною ознакою – розмір деталі. Кількісні ознаки можуть бути дискретними або неперервними.

Перевірку сукупності деталей можна провести 2 способами:

- Провести перевірку всіх деталей

- Перевірити лише певну частину деталей

Вибірковою сукупністю (вибіркою) назив. сукупність випадково взятих об’єктів.

Генеральною сукупністю назив сукупність об’єктів з яких зроблено вибірку.

Об’ємом сукупності (вибіркової або генеральної) назив кількість об’єктів цієї сукупності.

Вибірки можуть бути повторні та безповторні. Повторною назив вибірка, при якій відібраний об’єкт повертається до генеральної сукупності. Безповторна – коли об’єкт не повертається до генеральної сукупності.

Репрезентативна вибірка – представницька, коли її здійснюють випадково. Кожен об’єкт вибірки відібраний випадок з генеральної сукупності, якщо всі її об’єкти мають однакову ймовірність потрапити до вибірки.

62. Статистичні розподіли вибірок.

Для детального вивчення вибірки в простому статистичному ряді доцільно зробити обробку, згрупувати члени вибіркової сукупності, що приймають рівні значення, ознаки або значення в деякому інтервалі.

Нехай з генеральної сукупності взята вибірка об’єктів для вивчення ознаки Х, яка приймає значення х₁ – n₁ раз … х_m – m раз. Значення х₁… х_m - варіанти ознаки х. варіанти, що записані до таблиці у зростаючому порядку назив варіаційним рядом.

Кількість спостережень – n₁ , n₂ …n_m - назив рядом частот. Сума усіх частот назив об’ємом вибірки, обчислюється за формулою

Відношення частоти m_k до об’єму вибірки n_k назив відносною частотою варіант х_k. Сума всіх відносних частот вибірки = 1

– відносна частота варіант х_k . Статистичним розподілом вибірки назив перелік варіант та відповідних їм частот або відносних частот.

63. Емпірична функція розподілу, гістограма та полігон.

Емпірична функція розподілу або функція розподілу вибірки назив , яка визначає для кожного значення х відносну частоту події і за аналогією Х<х

Інтегральна функція розподілу F(x) генеральної сукупності назив теоретичною функцією розподілу, вона відрізняється від емпіричної тим, що визначає ймовірність події Х<х, а емпірична відносну частоту цієї події.

Властивості:

1) 0< <1

2) Зростаюча.

3) =

Полігоном частот називається ламана, відрізки якої з’єднують точки (x₁;n₁)(x₂;n₂)…(x_m; n_m); відносних частот (x₁; w₁) (x₂; w₂)…(x_m; w_m).

Гістограмою частот назив східчасту фігуру, яка складається з прямокутників основами яких є відрізки довжиною x_k-x_k-1, а висоти .

Гістограмою відносних частот назив східчасту фігуру, яка складається з прямокутників основами яких є відрізки довжиною x_k-x_k-1, а висоти - щільність частоти.

Площа гістограми частот = об’єму вибірки, а площа гістограми відносних частот = 1.

Гістограма – наближений графік диференціальної функції розподілу.

64. Числові характеристики: вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення.

Аналогічно математичному сподіванню, дисперсії та середньоквадратичному відхиленню ДВВ визначають вибіркові характеристики замінюючи при цьому ймовірність р_к на відносні частоти .

Простим середньоарифметичним вибірки називають суму всіх варіант поділену на об’єм вибірки , де n – об’єм вибірки, - варіант вибірки, де к= .

Вибірковим середнім або зваженим середньоарифметичним вибірки назив середнє арифметичне варіант вибірки із врахуванням їх відносних частоті позначається вибіркове середнє: =

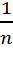
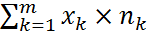
Вибіркове середнє аналогом математичного сподівання М(х) і використовується дуже часто, воно може приймати різні значення при різних вибірках однакового об’єму.

Основні властивості вибіркового середнього:

1) При множенні усіх варіант вибірки на однаковий множник, вибіркове середнє також множиться на цей множник = = С

2) Якщо до усіх варіант вибірки додати (відняти) однакове число, то вибіркове середнє збільшується (зменшується) на це число

Вибірковою дисперсією Дв назив середнє квадратичне відхилення варіант від вибіркового середнього із врахуванням їх відносних частот

Вибірковим середньоквадратичним відхиленням назив квадратний корінь із вибіркової дисперсії, його ще назив стандартом:

Вибіркова дисперсія дає занижені значення для дисперсії генеральної сукупності.

Математичне сподівання вибіркової дисперсії

М(Dв) =

Тому вибіркову дисперсію доцільно виправити таким чином, щоб вона стала незміщеною оцінкою. Для цього достатньо Dв до множити на .

Вибіркову дисперсію виправлену позначають ,

При великих об’ємах вибірки Dв і дисперсія генеральної сукупності мало відрізняються один від одного, тому виправлену дисперсію знаходять при об’ємах n<30.

65. Мода й медіана, емпіричні початкові та центральні моменти, асиметрія та ексцес.

Медіану вибірки позначають . Якщо обсяг статистичного матеріалу є непарним числом, тобто n =2*k+1, де k – натуральне число, то медіана = .

Якщо обсяг статистичного матеріалу є парним числом, тобто m=2*k, де k – натуральне число. То медіаною вважають величину .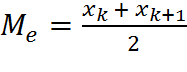

Модою статистичного матеріалу назив той елемент цієї вибірки, який найчастіше трапляється у ній. Моду вибірки позначають 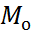. очевидно, що вибірка може мати кілька мод.

Початкові емпіричні моменти позначаються k=

Якщо перший емпіричний момент, то матимемо 1=

Відповідно, якщо другий, то 2=

Центральний момент

Третій та четвертий моменти застосовуються при знаходженні коефіцієнта асиметрії та ексцесу.

Асиметрія: Ексцес: = - 3

Якщо варіант статистичного розподілу вибірки симетрично розміщені щодо вибіркового середнього 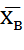, то в цьому випадку =0, оскільки 3 = 0.

При <0 варіант статистичного розподілу переважають, то таку асиметрію назив додатною.

66. Дати визначення статистичної оцінки.

Статистичною оцінкою θ* невідомого параметра θ теоретичного розподілу називається його найближче значення, що залежить від вибірки. Статистична оцінка називається незсунутою, якщо математичне сподівання дорівнює самому параметру. Статистична оцінка називається зсунутою, якщо математичне сподівання не дорівнює параметру генеральної сукупності. θ* тим точніше визначає θ, чим менша абсолютна величина θ- θ*.

67. Точкові та інтервальні статистичні оцінки.

Точковими оцінками параметрів генеральної сукупності називаються такі оцінки, які визначаються одним числом. До точкових оцінок відносять вибіркове середнє, вибіркова дисперсія, вибіркове середнє квадратичне відхилення. Якщо об’єм вибірки малий, то точкові оцінки задовольняють точкові потреби точності, якщо об’єм вибірки малий, то точкові оцінки можуть давати значні похибки, тому використовують інтервальні оцінки.

Інтервальною оцінкою називається оцінка, яка визначається двома числами, кінцями інтервала. Інтервальні оцінки дозволяють встановити точність та надійність оцінок.

68. Дати визначення довірчого інтервалу.

Довірчий інтервал — інтервал, у межах якого з заданою довірчою імовірністю можна чекати значення оцінюваної (шуканої) випадкової величини. Застосовується для більш повної оцінки точності в порівнянні з точковою оцінкою.

Інтервал називають довірчим, якщо він покриває невідомий параметр із заданою надійністю . Кінці довірчого інтервалу є випадковими величинами.

Нехай кількісна ознака х. Потрібно знайти довірчий інтервал, що покриває математичне сподівання заданому

Де , .

З надійністю довірчий інтервал покриває невідомий параметр a з точністю оцінки .

69. Що таке нульова та альтернативна статистичні гіпотези.

При дослідження вибірки можна зробити певні статистичні висновки про основні параметри або про закон розподілу генеральної сукупності.

Гіпотеза, яка підлягає перевірці назив основною або нульовою гіпотезою .

Поряд з нульовою гіпотезою існує альтернативна гіпотеза, яка заперечує нульову гіпотезу, позначається

Наприклад полягає в тому, що

Гіпотеза є простою (однозначною), а в другому випадку є складною, неоднозначною.

70. Перевірка (правдивості нульової) гіпотези про нормальний закон розподілу ознаки генеральної сукупності.

Для перевірки використовують спеціально підібрану ВВ к, точний або наближений розподіл, який відомий, і який назив статистичним критерієм узгодження, тобто статистичний критерій – це правило за яким гіпотеза приймається або відхиляється. Гіпотеза полягає в тому, що (рівність вибіркових дисперсій генеральних сукупностей). В якості критерію к обирають відношення виправлених дисперсій - ВВ, яка розподілена за законом Фішера- Снедикора спостережне значення позначають назив значення критерію обчислення за вибіркою.

Основні принципи перевірки статистичної гіпотези

Якщо спостережне значення критерію належить критичній області, то гіпотезу відкидають.

Якщо спостережне значення критерію належить області прийняття гіпотези – гіпотезу приймають.

Оскільки критерій К одновимірна ВВ та всі її можливі значення належать деякому інтервалу.

Аналогічно критична область і область прийняття гіпотези є також інтервалами, тому існують точки, які поділяють ці інтервали, їх називають критичними точками .

Розрізняють одно і двосторонню критичну область.

1) Якщо К > 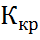( 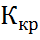> 0) – правостороння критична область

2) Якщо К < 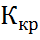( 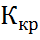< 0) – лівостороння критична область

3) Якщо 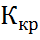К< , К> 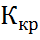– двостороння критична область

Для перевірки гіпотези про закон розподілу необхідно мати значення емпіричних та теоретичних частот. Емпіричними назив частоти, які спостерігаються при реалізації вибірки, а теоретичні – це частоти, які обчислюють за формами припущень висунутих гіпотез про закон розподілу.

71. Емпіричні та теоретичні частоти.

Для перевірки гіпотези про закон розподілу необхідно мати значення емпіричних та теоретичних частот. Емпіричними назив частоти, які спостерігаються при реалізації вибірки, а теоретичні – це частоти, які обчислюють за формами припущень висунутих гіпотез про закон розподілу.

72. Критерії узгодження Пірсона та Колмогорова.

Критерій Пірсона:

застосовується не тільки для перевірки інших законів розподілу. Цей критерій не доводить справедливості гіпотези, а встановлює на прийнятому рівні значущості її узгодження або неузгодження з даним спостереженням.

Правило Пірсона: При заданому рівні значущості 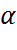перевірити : генеральна сукупність має нормальний закон розподілу.

1) Обчислити теоретичні частоти для варіант вибірки

,

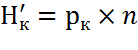де = Р(х= 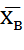), , де h- довжина часткового інтервалу.

2) Обчислити спостережне значення

K= S – 1 – r, де S – кількість інтервалів вибірки;

r – кількість параметрів закону розподілу.

3) Знайти з таблиці критичні точки , яка залежить від рівня значущості і ступеня свободи.

4) Порівняти і і зробити висновки.

Якщо < , то гіпотезу про нормальний закон розподілу слід прийняти.

Якщо > , то гіпотезу слід відхилити.

У статистиці критерій узгодженості Колмогорова (також відомий, як критерій узгодженості Колмогорова — Смирнова) використовується для того, щоб визначити, чи підкоряються два емпіричних розподіли одному закону, або визначити, чи підкоряється одержаний розподіл деякій моделі.

Критерій Колмогорова заснований на визначенні максимальної розбіжності між накопиченими частотами і частості емпіричних і теоретичних розподілів:

або,

де D і d - відповідно максимальна різниця між накопиченими частотами і накопиченими частості емпіричного і теоретичного рядів розподілів;

N - число одиниць сукупності.

Розрахувавши значення l, за таблицею Р (l) визначають ймовірність, з якою можна стверджувати, що відхилення емпіричних частот від теоретичних випадкові. Ймовірність Р (l) може змінюватися від 0 до 1. При Р (l) = 1 відбувається повний збіг частот, Р (l) = 0 - повна розбіжність. Якщо l приймає значення до 0,3, то Р (l) = 1.

Основна умова використання критерію Колмогорова - досить велике число спостережень.

73. Див 72

Дата добавления: 2015-10-31